HyperVAE: A Minimum Description Length Variational Hyper-Encoding Network

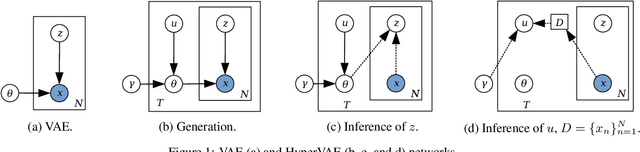
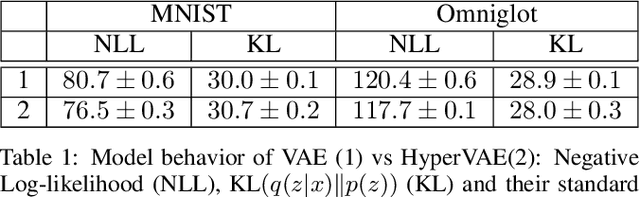
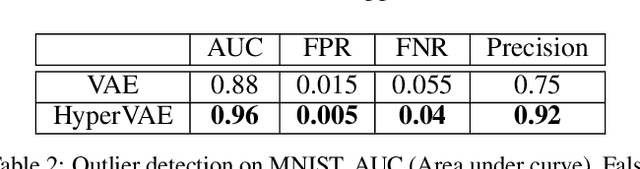
We propose a framework called HyperVAE for encoding distributions of distributions. When a target distribution is modeled by a VAE, its neural network parameters \theta is drawn from a distribution p(\theta) which is modeled by a hyper-level VAE. We propose a variational inference using Gaussian mixture models to implicitly encode the parameters \theta into a low dimensional Gaussian distribution. Given a target distribution, we predict the posterior distribution of the latent code, then use a matrix-network decoder to generate a posterior distribution q(\theta). HyperVAE can encode the parameters \theta in full in contrast to common hyper-networks practices, which generate only the scale and bias vectors as target-network parameters. Thus HyperVAE preserves much more information about the model for each task in the latent space. We discuss HyperVAE using the minimum description length (MDL) principle and show that it helps HyperVAE to generalize. We evaluate HyperVAE in density estimation tasks, outlier detection and discovery of novel design classes, demonstrating its efficacy.