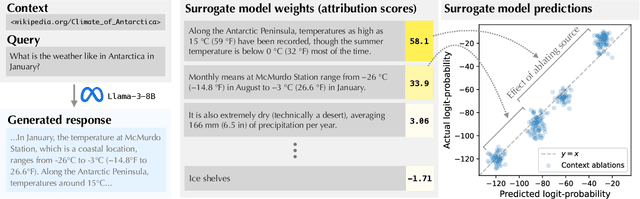
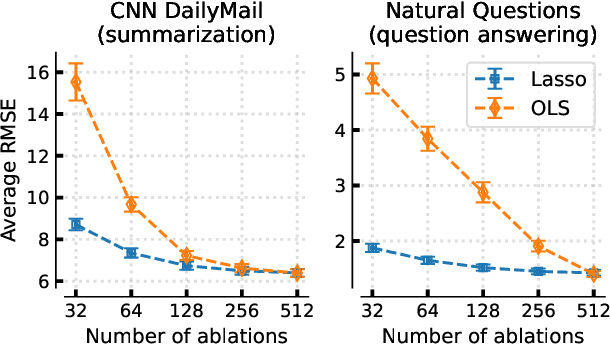
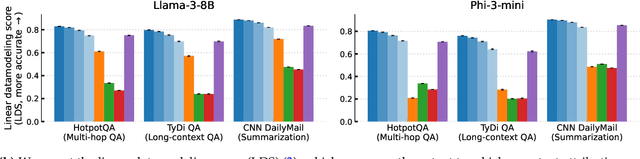
ContextCite: Attributing Model Generation to Context

How do language models use information provided as context when generating a response? Can we infer whether a particular generated statement is actually grounded in the context, a misinterpretation, or fabricated? To help answer these questions, we introduce the problem of context attribution: pinpointing the parts of the context (if any) that led a model to generate a particular statement. We then present ContextCite, a simple and scalable method for context attribution that can be applied on top of any existing language model. Finally, we showcase the utility of ContextCite through three applications: (1) helping verify generated statements (2) improving response quality by pruning the context and (3) detecting poisoning attacks. We provide code for ContextCite at https://github.com/MadryLab/context-cite.

Decomposing and Editing Predictions by Modeling Model Computation

How does the internal computation of a machine learning model transform inputs into predictions? In this paper, we introduce a task called component modeling that aims to address this question. The goal of component modeling is to decompose an ML model's prediction in terms of its components -- simple functions (e.g., convolution filters, attention heads) that are the "building blocks" of model computation. We focus on a special case of this task, component attribution, where the goal is to estimate the counterfactual impact of individual components on a given prediction. We then present COAR, a scalable algorithm for estimating component attributions; we demonstrate its effectiveness across models, datasets, and modalities. Finally, we show that component attributions estimated with COAR directly enable model editing across five tasks, namely: fixing model errors, ``forgetting'' specific classes, boosting subpopulation robustness, localizing backdoor attacks, and improving robustness to typographic attacks. We provide code for COAR at https://github.com/MadryLab/modelcomponents .

ModelDiff: A Framework for Comparing Learning Algorithms

We study the problem of (learning) algorithm comparison, where the goal is to find differences between models trained with two different learning algorithms. We begin by formalizing this goal as one of finding distinguishing feature transformations, i.e., input transformations that change the predictions of models trained with one learning algorithm but not the other. We then present ModelDiff, a method that leverages the datamodels framework (Ilyas et al., 2022) to compare learning algorithms based on how they use their training data. We demonstrate ModelDiff through three case studies, comparing models trained with/without data augmentation, with/without pre-training, and with different SGD hyperparameters. Our code is available at https://github.com/MadryLab/modeldiff .

Do Input Gradients Highlight Discriminative Features?

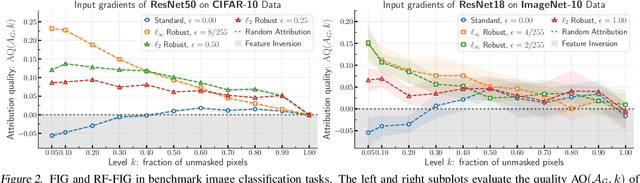
Interpretability methods that seek to explain instance-specific model predictions [Simonyan et al. 2014, Smilkov et al. 2017] are often based on the premise that the magnitude of input-gradient -- gradient of the loss with respect to input -- highlights discriminative features that are relevant for prediction over non-discriminative features that are irrelevant for prediction. In this work, we introduce an evaluation framework to study this hypothesis for benchmark image classification tasks, and make two surprising observations on CIFAR-10 and Imagenet-10 datasets: (a) contrary to conventional wisdom, input gradients of standard models (i.e., trained on the original data) actually highlight irrelevant features over relevant features; (b) however, input gradients of adversarially robust models (i.e., trained on adversarially perturbed data) starkly highlight relevant features over irrelevant features. To better understand input gradients, we introduce a synthetic testbed and theoretically justify our counter-intuitive empirical findings. Our observations motivate the need to formalize and verify common assumptions in interpretability, while our evaluation framework and synthetic dataset serve as a testbed to rigorously analyze instance-specific interpretability methods.

The Pitfalls of Simplicity Bias in Neural Networks

Several works have proposed Simplicity Bias (SB)---the tendency of standard training procedures such as Stochastic Gradient Descent (SGD) to find simple models---to justify why neural networks generalize well [Arpit et al. 2017, Nakkiran et al. 2019, Valle-Perez et al. 2019]. However, the precise notion of simplicity remains vague. Furthermore, previous settings that use SB to justify why neural networks generalize well do not simultaneously capture the brittleness of neural networks---a widely observed phenomenon in practice [Goodfellow et al. 2014, Jo and Bengio 2017]. To this end, we introduce a collection of piecewise-linear and image-based datasets that (a) naturally incorporate a precise notion of simplicity and (b) capture the subtleties of neural networks trained on real datasets. Through theory and experiments on these datasets, we show that SB of SGD and variants is extreme: neural networks rely exclusively on the simplest feature and remain invariant to all predictive complex features. Consequently, the extreme nature of SB explains why seemingly benign distribution shifts and small adversarial perturbations significantly degrade model performance. Moreover, contrary to conventional wisdom, SB can also hurt generalization on the same data distribution, as SB persists even when the simplest feature has less predictive power than the more complex features. We also demonstrate that common approaches for improving generalization and robustness---ensembles and adversarial training---do not mitigate SB and its shortcomings. Given the central role played by SB in generalization and robustness, we hope that the datasets and methods in this paper serve as an effective testbed to evaluate novel algorithmic approaches aimed at avoiding the pitfalls of extreme SB.

Number of Connected Components in a Graph: Estimation via Counting Patterns

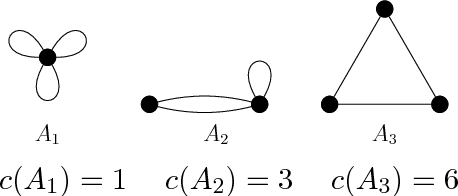
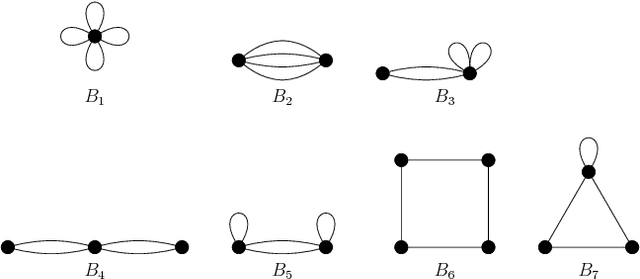
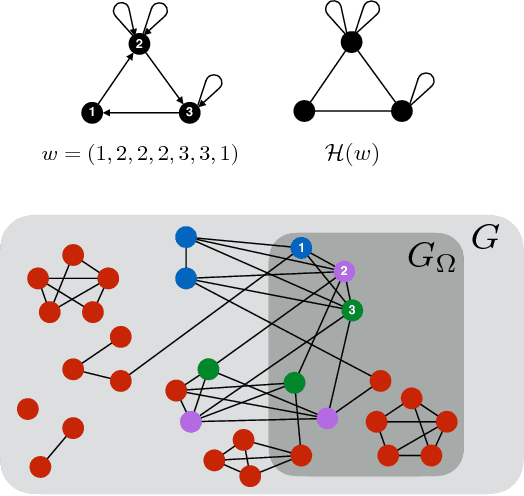
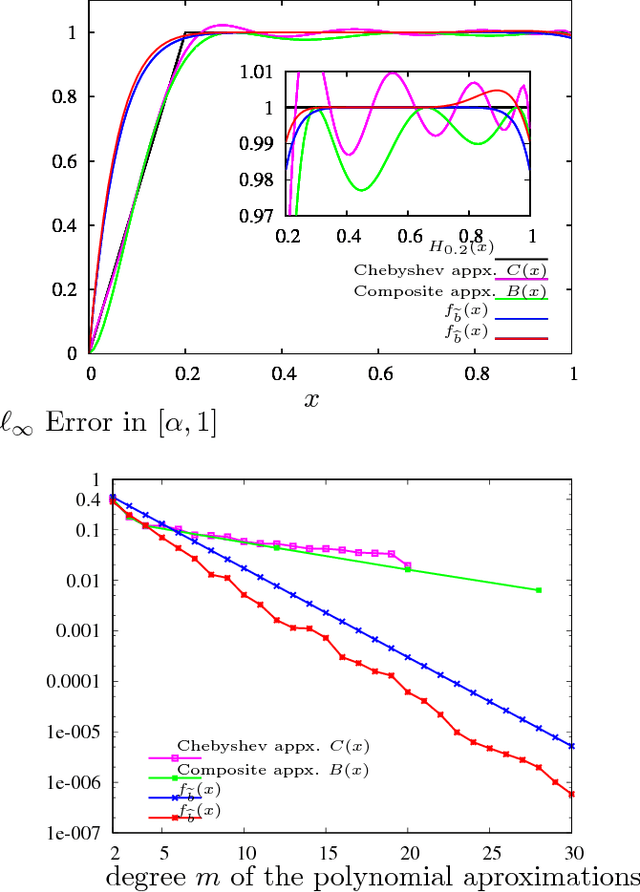
Due to the limited resources and the scale of the graphs in modern datasets, we often get to observe a sampled subgraph of a larger original graph of interest, whether it is the worldwide web that has been crawled or social connections that have been surveyed. Inferring a global property of the original graph from such a sampled subgraph is of a fundamental interest. In this work, we focus on estimating the number of connected components. It is a challenging problem and, for general graphs, little is known about the connection between the observed subgraph and the number of connected components of the original graph. In order to make this connection, we propose a highly redundant and large-dimensional representation of the subgraph, which at first glance seems counter-intuitive. A subgraph is represented by the counts of patterns, known as network motifs. This representation is crucial in introducing a novel estimator for the number of connected components for general graphs, under the knowledge of the spectral gap of the original graph. The connection is made precise via the Schatten $k$-norms of the graph Laplacian and the spectral representation of the number of connected components. We provide a guarantee on the resulting mean squared error that characterizes the bias variance tradeoff. Experiments on synthetic and real-world graphs suggest that we improve upon competing algorithms for graphs with spectral gaps bounded away from zero.