Number of Connected Components in a Graph: Estimation via Counting Patterns

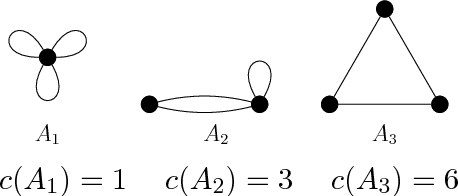
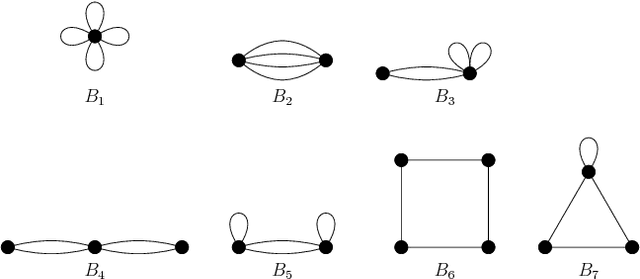
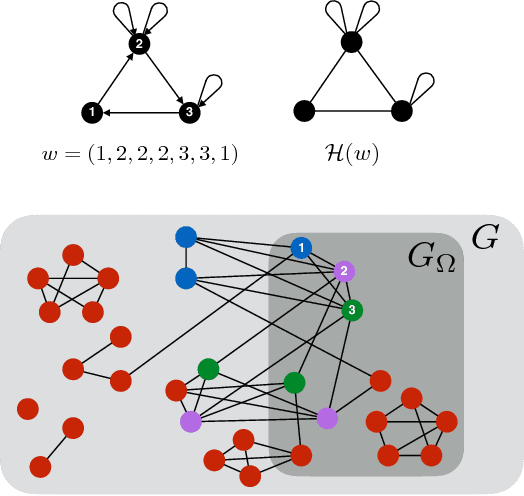
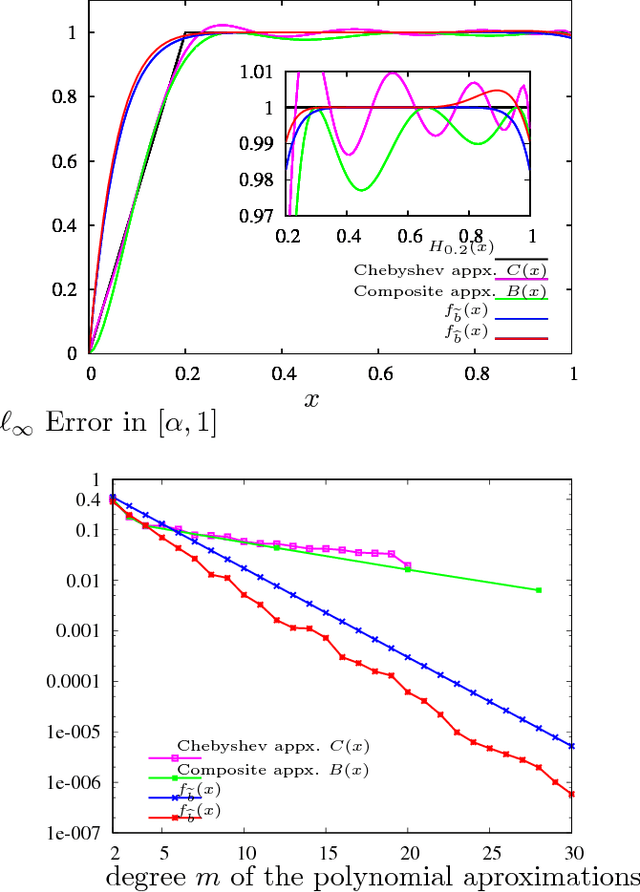
Due to the limited resources and the scale of the graphs in modern datasets, we often get to observe a sampled subgraph of a larger original graph of interest, whether it is the worldwide web that has been crawled or social connections that have been surveyed. Inferring a global property of the original graph from such a sampled subgraph is of a fundamental interest. In this work, we focus on estimating the number of connected components. It is a challenging problem and, for general graphs, little is known about the connection between the observed subgraph and the number of connected components of the original graph. In order to make this connection, we propose a highly redundant and large-dimensional representation of the subgraph, which at first glance seems counter-intuitive. A subgraph is represented by the counts of patterns, known as network motifs. This representation is crucial in introducing a novel estimator for the number of connected components for general graphs, under the knowledge of the spectral gap of the original graph. The connection is made precise via the Schatten $k$-norms of the graph Laplacian and the spectral representation of the number of connected components. We provide a guarantee on the resulting mean squared error that characterizes the bias variance tradeoff. Experiments on synthetic and real-world graphs suggest that we improve upon competing algorithms for graphs with spectral gaps bounded away from zero.