Hanzhang Hu
Efficient Forward Architecture Search
May 31, 2019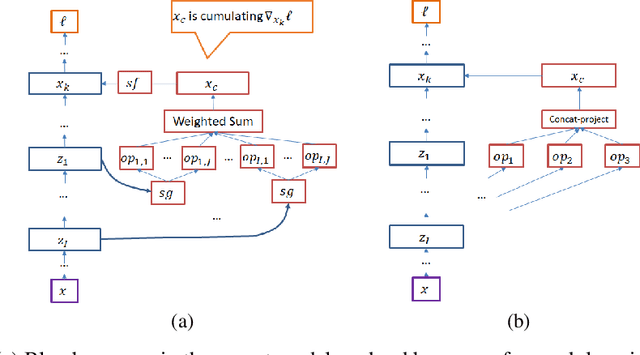
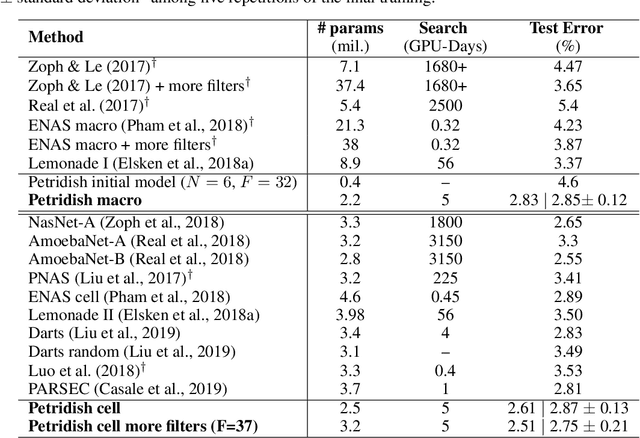
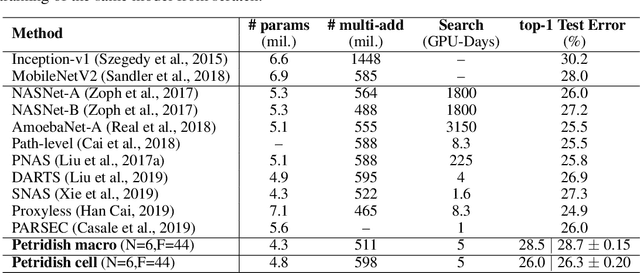
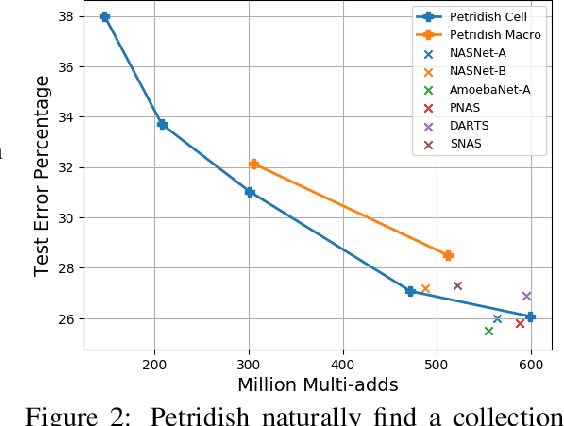
Abstract:We propose a neural architecture search (NAS) algorithm, Petridish, to iteratively add shortcut connections to existing network layers. The added shortcut connections effectively perform gradient boosting on the augmented layers. The proposed algorithm is motivated by the feature selection algorithm forward stage-wise linear regression, since we consider NAS as a generalization of feature selection for regression, where NAS selects shortcuts among layers instead of selecting features. In order to reduce the number of trials of possible connection combinations, we train jointly all possible connections at each stage of growth while leveraging feature selection techniques to choose a subset of them. We experimentally show this process to be an efficient forward architecture search algorithm that can find competitive models using few GPU days in both the search space of repeatable network modules (cell-search) and the space of general networks (macro-search). Petridish is particularly well-suited for warm-starting from existing models crucial for lifelong-learning scenarios.
Learning Anytime Predictions in Neural Networks via Adaptive Loss Balancing
May 25, 2018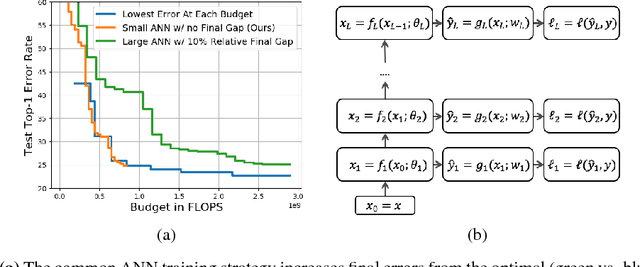
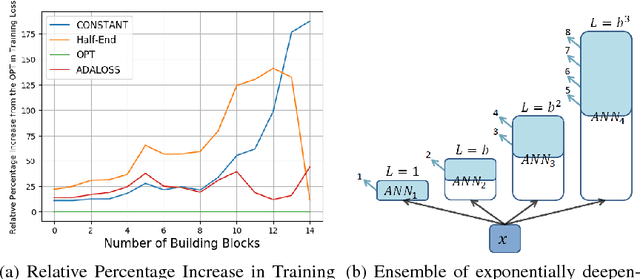

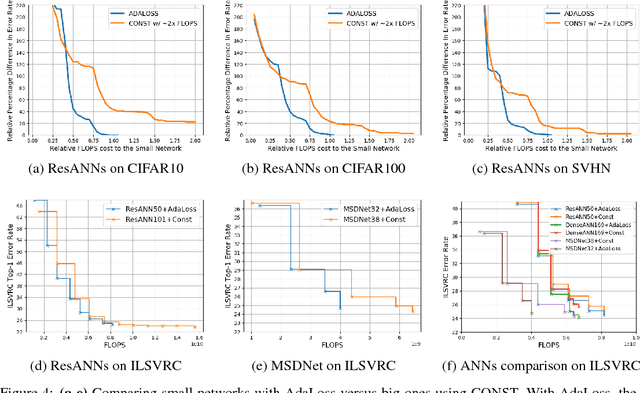
Abstract:This work considers the trade-off between accuracy and test-time computational cost of deep neural networks (DNNs) via \emph{anytime} predictions from auxiliary predictions. Specifically, we optimize auxiliary losses jointly in an \emph{adaptive} weighted sum, where the weights are inversely proportional to average of each loss. Intuitively, this balances the losses to have the same scale. We demonstrate theoretical considerations that motivate this approach from multiple viewpoints, including connecting it to optimizing the geometric mean of the expectation of each loss, an objective that ignores the scale of losses. Experimentally, the adaptive weights induce more competitive anytime predictions on multiple recognition data-sets and models than non-adaptive approaches including weighing all losses equally. In particular, anytime neural networks (ANNs) can achieve the same accuracy faster using adaptive weights on a small network than using static constant weights on a large one. For problems with high performance saturation, we also show a sequence of exponentially deepening ANNscan achieve near-optimal anytime results at any budget, at the cost of a const fraction of extra computation.
Log-DenseNet: How to Sparsify a DenseNet
Oct 30, 2017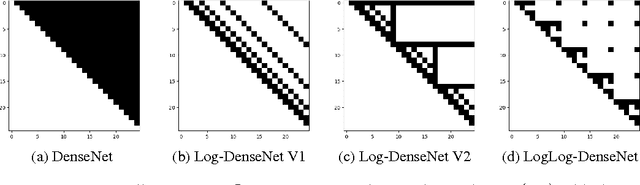
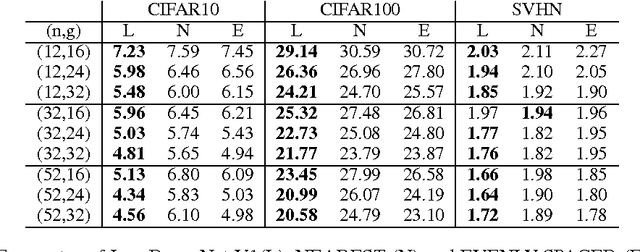
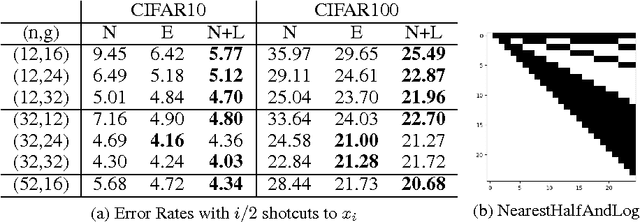
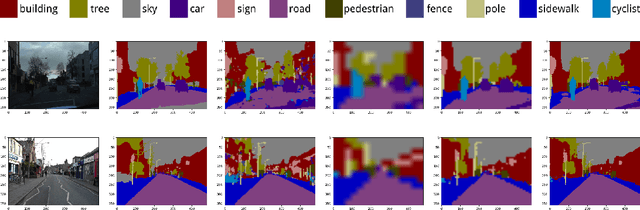
Abstract:Skip connections are increasingly utilized by deep neural networks to improve accuracy and cost-efficiency. In particular, the recent DenseNet is efficient in computation and parameters, and achieves state-of-the-art predictions by directly connecting each feature layer to all previous ones. However, DenseNet's extreme connectivity pattern may hinder its scalability to high depths, and in applications like fully convolutional networks, full DenseNet connections are prohibitively expensive. This work first experimentally shows that one key advantage of skip connections is to have short distances among feature layers during backpropagation. Specifically, using a fixed number of skip connections, the connection patterns with shorter backpropagation distance among layers have more accurate predictions. Following this insight, we propose a connection template, Log-DenseNet, which, in comparison to DenseNet, only slightly increases the backpropagation distances among layers from 1 to ($1 + \log_2 L$), but uses only $L\log_2 L$ total connections instead of $O(L^2)$. Hence, Log-DenseNets are easier than DenseNets to implement and to scale. We demonstrate the effectiveness of our design principle by showing better performance than DenseNets on tabula rasa semantic segmentation, and competitive results on visual recognition.
Gradient Boosting on Stochastic Data Streams
Mar 01, 2017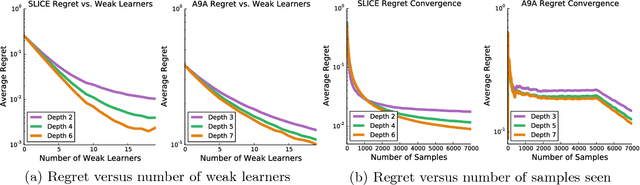
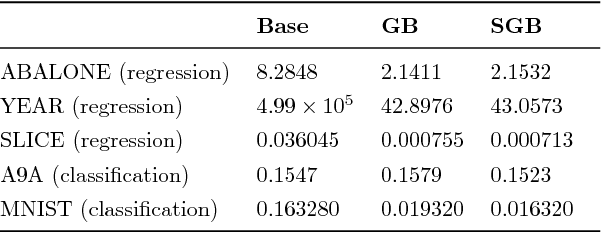
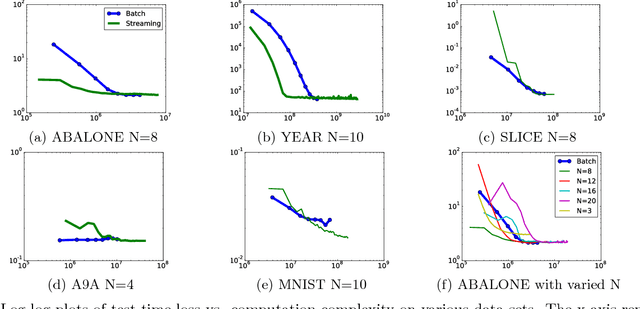
Abstract:Boosting is a popular ensemble algorithm that generates more powerful learners by linearly combining base models from a simpler hypothesis class. In this work, we investigate the problem of adapting batch gradient boosting for minimizing convex loss functions to online setting where the loss at each iteration is i.i.d sampled from an unknown distribution. To generalize from batch to online, we first introduce the definition of online weak learning edge with which for strongly convex and smooth loss functions, we present an algorithm, Streaming Gradient Boosting (SGB) with exponential shrinkage guarantees in the number of weak learners. We further present an adaptation of SGB to optimize non-smooth loss functions, for which we derive a O(ln N/N) convergence rate. We also show that our analysis can extend to adversarial online learning setting under a stronger assumption that the online weak learning edge will hold in adversarial setting. We finally demonstrate experimental results showing that in practice our algorithms can achieve competitive results as classic gradient boosting while using less computation.
Efficient Feature Group Sequencing for Anytime Linear Prediction
Dec 05, 2016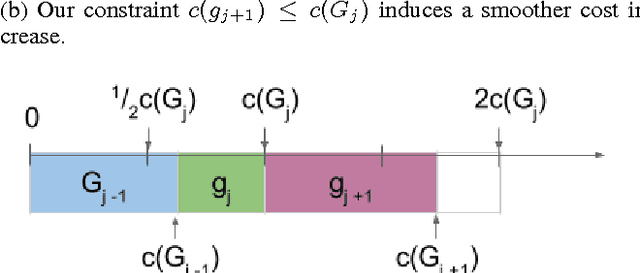

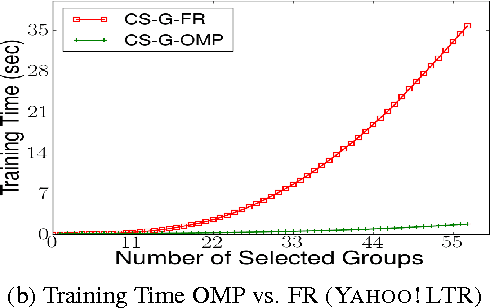
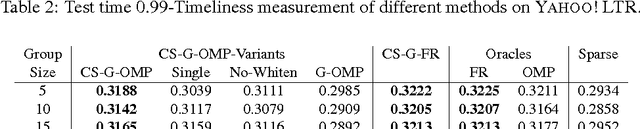
Abstract:We consider \textit{anytime} linear prediction in the common machine learning setting, where features are in groups that have costs. We achieve anytime (or interruptible) predictions by sequencing the computation of feature groups and reporting results using the computed features at interruption. We extend Orthogonal Matching Pursuit (OMP) and Forward Regression (FR) to learn the sequencing greedily under this group setting with costs. We theoretically guarantee that our algorithms achieve near-optimal linear predictions at each budget when a feature group is chosen. With a novel analysis of OMP, we improve its theoretical bound to the same strength as that of FR. In addition, we develop a novel algorithm that consumes cost $4B$ to approximate the optimal performance of \textit{any} cost $B$, and prove that with cost less than $4B$, such an approximation is impossible. To our knowledge, these are the first anytime bounds at \textit{all} budgets. We test our algorithms on two real-world data-sets and evaluate them in terms of anytime linear prediction performance against cost-weighted Group Lasso and alternative greedy algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge