ABCDE: Application-Based Cluster Diff Evals

This paper considers the problem of evaluating clusterings of very large populations of items. Given two clusterings, namely a Baseline clustering and an Experiment clustering, the tasks are twofold: 1) characterize their differences, and 2) determine which clustering is better. ABCDE is a novel evaluation technique for accomplishing that. It aims to be practical: it allows items to have associated importance values that are application-specific, it is frugal in its use of human judgements when determining which clustering is better, and it can report metrics for arbitrary slices of items, thereby facilitating understanding and debugging. The approach to measuring the delta in the clustering quality is novel: instead of trying to construct an expensive ground truth up front and evaluating the each clustering with respect to that, where the ground truth must effectively pre-anticipate clustering changes, ABCDE samples questions for judgement on the basis of the actual diffs between the clusterings. ABCDE builds upon the pointwise metrics for clustering evaluation, which make the ABCDE metrics intuitive and simple to understand. The mathematical elegance of the pointwise metrics equip ABCDE with rigorous yet practical ways to explore the clustering diffs and to estimate the quality delta.

Efficient Feature Group Sequencing for Anytime Linear Prediction

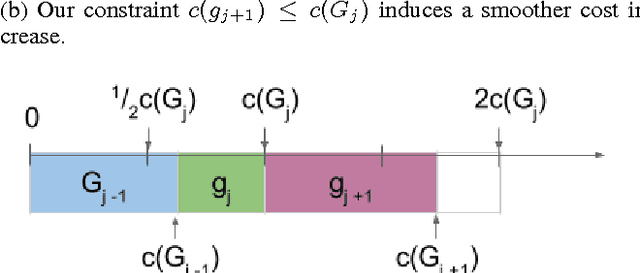
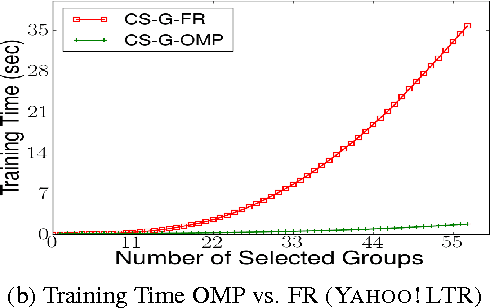
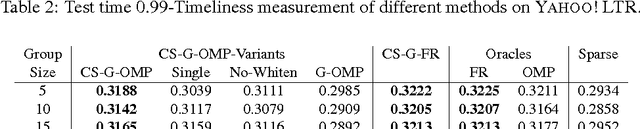
We consider \textit{anytime} linear prediction in the common machine learning setting, where features are in groups that have costs. We achieve anytime (or interruptible) predictions by sequencing the computation of feature groups and reporting results using the computed features at interruption. We extend Orthogonal Matching Pursuit (OMP) and Forward Regression (FR) to learn the sequencing greedily under this group setting with costs. We theoretically guarantee that our algorithms achieve near-optimal linear predictions at each budget when a feature group is chosen. With a novel analysis of OMP, we improve its theoretical bound to the same strength as that of FR. In addition, we develop a novel algorithm that consumes cost $4B$ to approximate the optimal performance of \textit{any} cost $B$, and prove that with cost less than $4B$, such an approximation is impossible. To our knowledge, these are the first anytime bounds at \textit{all} budgets. We test our algorithms on two real-world data-sets and evaluate them in terms of anytime linear prediction performance against cost-weighted Group Lasso and alternative greedy algorithms.

SpeedMachines: Anytime Structured Prediction

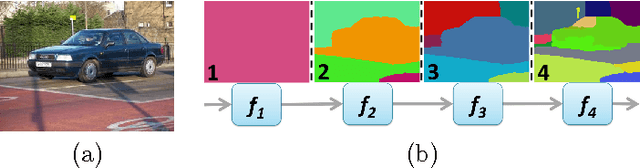
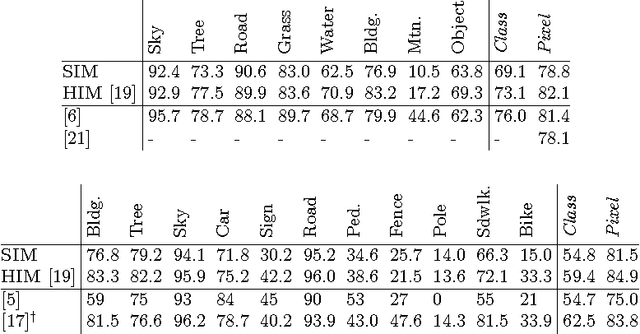
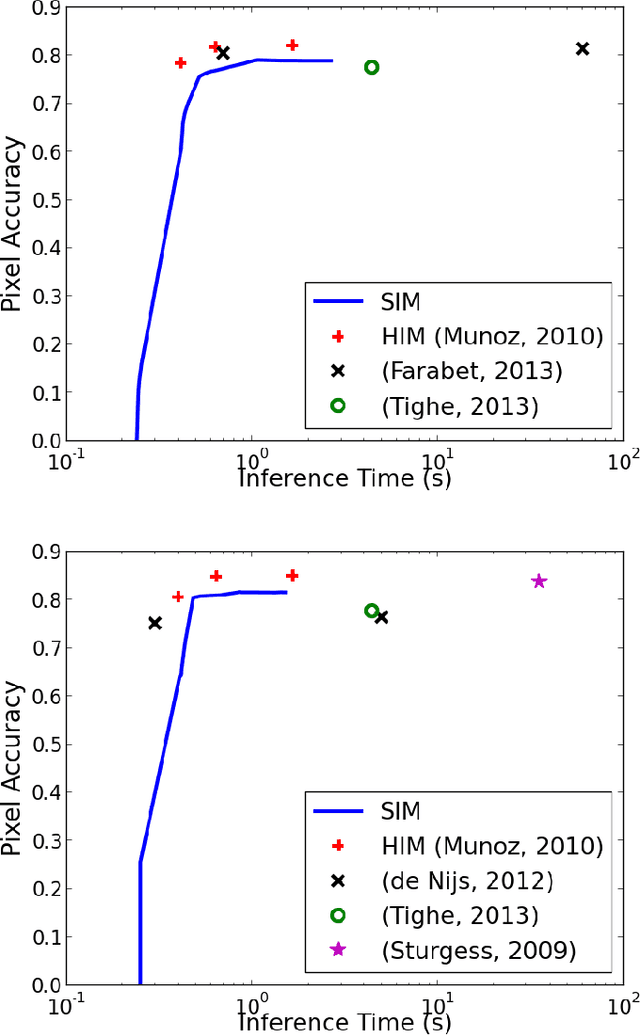
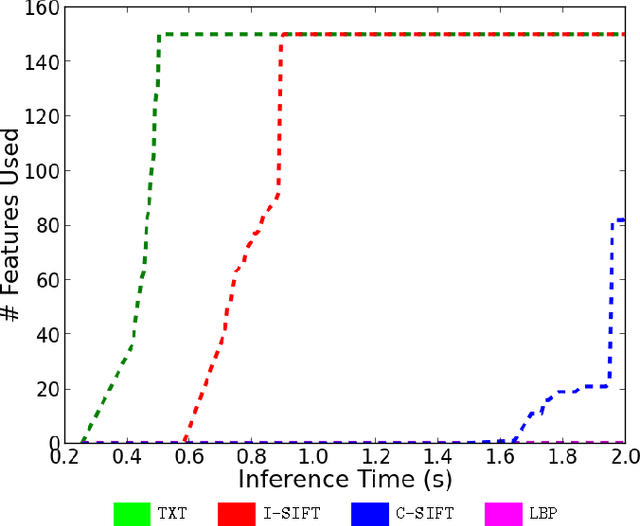
Structured prediction plays a central role in machine learning applications from computational biology to computer vision. These models require significantly more computation than unstructured models, and, in many applications, algorithms may need to make predictions within a computational budget or in an anytime fashion. In this work we propose an anytime technique for learning structured prediction that, at training time, incorporates both structural elements and feature computation trade-offs that affect test-time inference. We apply our technique to the challenging problem of scene understanding in computer vision and demonstrate efficient and anytime predictions that gradually improve towards state-of-the-art classification performance as the allotted time increases.

Generalized Boosting Algorithms for Convex Optimization

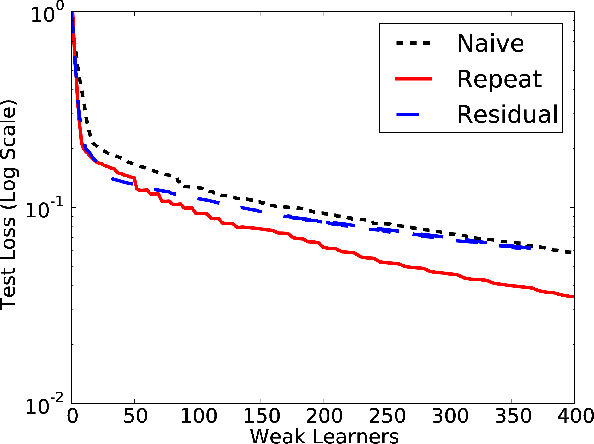
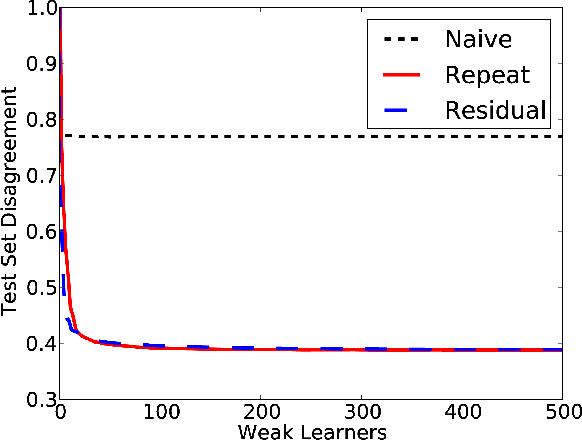
Boosting is a popular way to derive powerful learners from simpler hypothesis classes. Following previous work (Mason et al., 1999; Friedman, 2000) on general boosting frameworks, we analyze gradient-based descent algorithms for boosting with respect to any convex objective and introduce a new measure of weak learner performance into this setting which generalizes existing work. We present the weak to strong learning guarantees for the existing gradient boosting work for strongly-smooth, strongly-convex objectives under this new measure of performance, and also demonstrate that this work fails for non-smooth objectives. To address this issue, we present new algorithms which extend this boosting approach to arbitrary convex loss functions and give corresponding weak to strong convergence results. In addition, we demonstrate experimental results that support our analysis and demonstrate the need for the new algorithms we present.