Simple Linear Neuron Boosting

Given a differentiable network architecture and loss function, we revisit optimizing the network's neurons in function space using Boosted Backpropagation (Grubb & Bagnell, 2010), in contrast to optimizing in parameter space. From this perspective, we reduce descent in the space of linear functions that optimizes the network's backpropagated-errors to a preconditioned gradient descent algorithm. We show that this preconditioned update rule is equivalent to reparameterizing the network to whiten each neuron's features, with the benefit that the normalization occurs outside of inference. In practice, we use this equivalence to construct an online estimator for approximating the preconditioner and we propose an online, matrix-free learning algorithm with adaptive step sizes. The algorithm is applicable whenever autodifferentiation is available, including convolutional networks and transformers, and it is simple to implement for both the local and distributed training settings. We demonstrate fast convergence both in terms of epochs and wall clock time on a variety of tasks and networks.

SpeedMachines: Anytime Structured Prediction

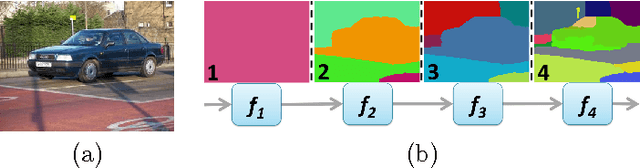
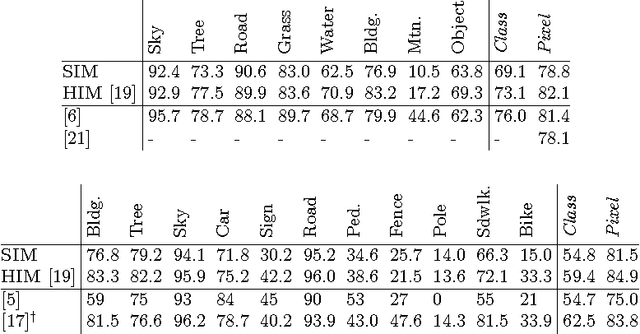
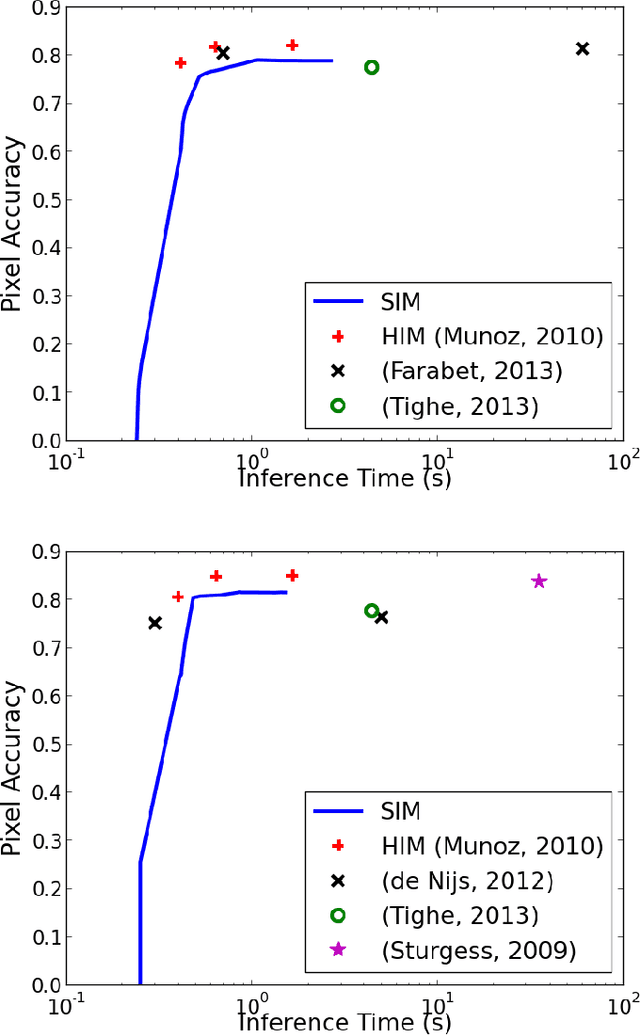
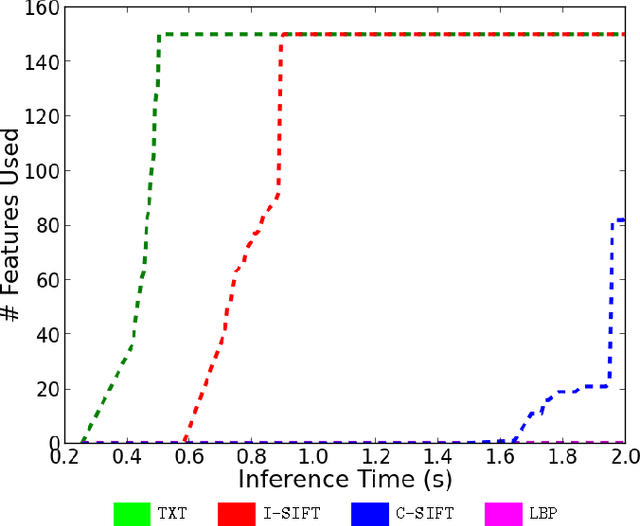
Structured prediction plays a central role in machine learning applications from computational biology to computer vision. These models require significantly more computation than unstructured models, and, in many applications, algorithms may need to make predictions within a computational budget or in an anytime fashion. In this work we propose an anytime technique for learning structured prediction that, at training time, incorporates both structural elements and feature computation trade-offs that affect test-time inference. We apply our technique to the challenging problem of scene understanding in computer vision and demonstrate efficient and anytime predictions that gradually improve towards state-of-the-art classification performance as the allotted time increases.