Efficient Feature Group Sequencing for Anytime Linear Prediction
Paper and Code
Dec 05, 2016

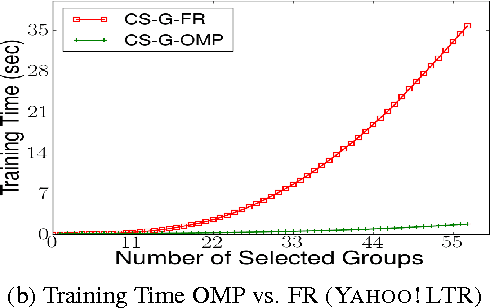
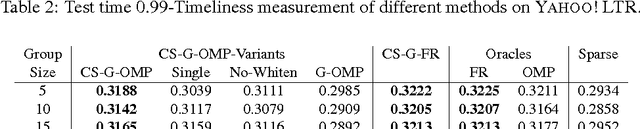
We consider \textit{anytime} linear prediction in the common machine learning setting, where features are in groups that have costs. We achieve anytime (or interruptible) predictions by sequencing the computation of feature groups and reporting results using the computed features at interruption. We extend Orthogonal Matching Pursuit (OMP) and Forward Regression (FR) to learn the sequencing greedily under this group setting with costs. We theoretically guarantee that our algorithms achieve near-optimal linear predictions at each budget when a feature group is chosen. With a novel analysis of OMP, we improve its theoretical bound to the same strength as that of FR. In addition, we develop a novel algorithm that consumes cost $4B$ to approximate the optimal performance of \textit{any} cost $B$, and prove that with cost less than $4B$, such an approximation is impossible. To our knowledge, these are the first anytime bounds at \textit{all} budgets. We test our algorithms on two real-world data-sets and evaluate them in terms of anytime linear prediction performance against cost-weighted Group Lasso and alternative greedy algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge