Learning Anytime Predictions in Neural Networks via Adaptive Loss Balancing
Paper and Code
May 25, 2018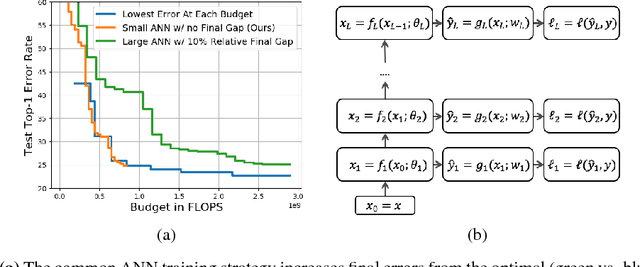
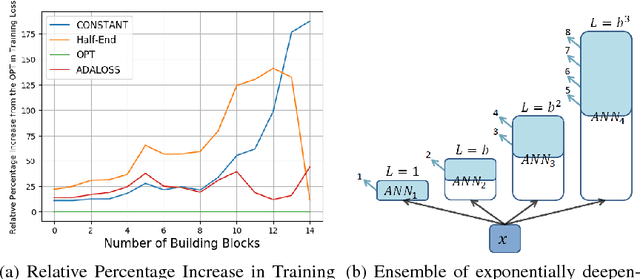

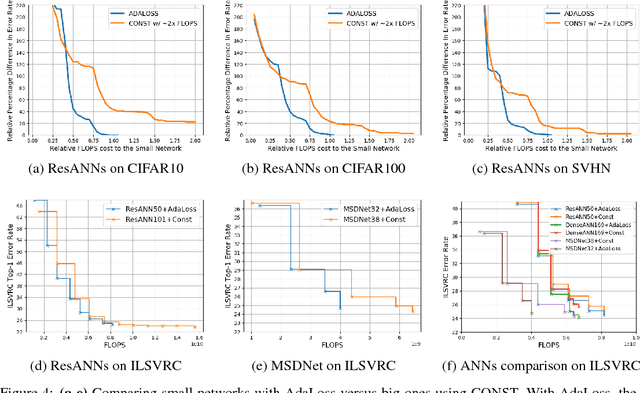
This work considers the trade-off between accuracy and test-time computational cost of deep neural networks (DNNs) via \emph{anytime} predictions from auxiliary predictions. Specifically, we optimize auxiliary losses jointly in an \emph{adaptive} weighted sum, where the weights are inversely proportional to average of each loss. Intuitively, this balances the losses to have the same scale. We demonstrate theoretical considerations that motivate this approach from multiple viewpoints, including connecting it to optimizing the geometric mean of the expectation of each loss, an objective that ignores the scale of losses. Experimentally, the adaptive weights induce more competitive anytime predictions on multiple recognition data-sets and models than non-adaptive approaches including weighing all losses equally. In particular, anytime neural networks (ANNs) can achieve the same accuracy faster using adaptive weights on a small network than using static constant weights on a large one. For problems with high performance saturation, we also show a sequence of exponentially deepening ANNscan achieve near-optimal anytime results at any budget, at the cost of a const fraction of extra computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge