Gradient Boosting on Stochastic Data Streams
Paper and Code
Mar 01, 2017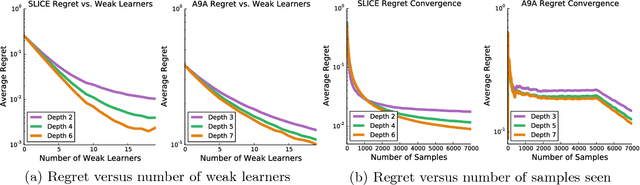
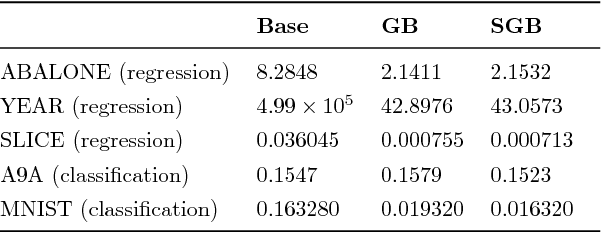
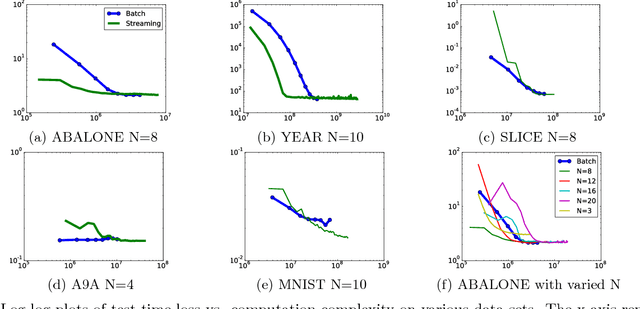
Boosting is a popular ensemble algorithm that generates more powerful learners by linearly combining base models from a simpler hypothesis class. In this work, we investigate the problem of adapting batch gradient boosting for minimizing convex loss functions to online setting where the loss at each iteration is i.i.d sampled from an unknown distribution. To generalize from batch to online, we first introduce the definition of online weak learning edge with which for strongly convex and smooth loss functions, we present an algorithm, Streaming Gradient Boosting (SGB) with exponential shrinkage guarantees in the number of weak learners. We further present an adaptation of SGB to optimize non-smooth loss functions, for which we derive a O(ln N/N) convergence rate. We also show that our analysis can extend to adversarial online learning setting under a stronger assumption that the online weak learning edge will hold in adversarial setting. We finally demonstrate experimental results showing that in practice our algorithms can achieve competitive results as classic gradient boosting while using less computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge