Physics-Informed GNN for non-linear constrained optimization: PINCO a solver for the AC-optimal power flow

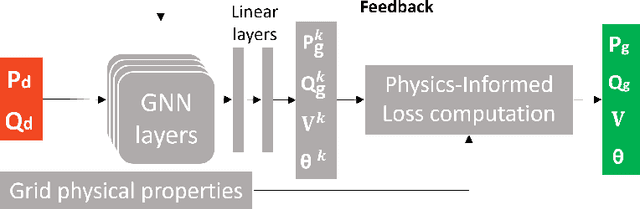
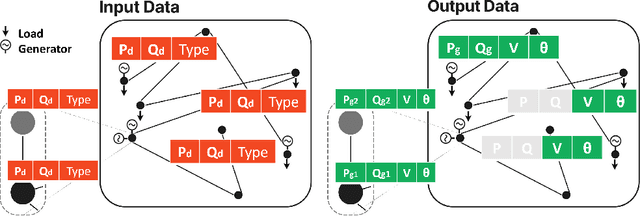
The energy transition is driving the integration of large shares of intermittent power sources in the electric power grid. Therefore, addressing the AC optimal power flow (AC-OPF) effectively becomes increasingly essential. The AC-OPF, which is a fundamental optimization problem in power systems, must be solved more frequently to ensure the safe and cost-effective operation of power systems. Due to its non-linear nature, AC-OPF is often solved in its linearized form, despite inherent inaccuracies. Non-linear solvers, such as the interior point method, are typically employed to solve the full OPF problem. However, these iterative methods may not converge for large systems and do not guarantee global optimality. This work explores a physics-informed graph neural network, PINCO, to solve the AC-OPF. We demonstrate that this method provides accurate solutions in a fraction of the computational time when compared to the established non-linear programming solvers. Remarkably, PINCO generalizes effectively across a diverse set of loading conditions in the power system. We show that our method can solve the AC-OPF without violating inequality constraints. Furthermore, it can function both as a solver and as a hybrid universal function approximator. Moreover, the approach can be easily adapted to different power systems with minimal adjustments to the hyperparameters, including systems with multiple generators at each bus. Overall, this work demonstrates an advancement in the field of power system optimization to tackle the challenges of the energy transition. The code and data utilized in this paper are available at https://anonymous.4open.science/r/opf_pinn_iclr-B83E/.

Mesh-Informed Reduced Order Models for Aneurysm Rupture Risk Prediction

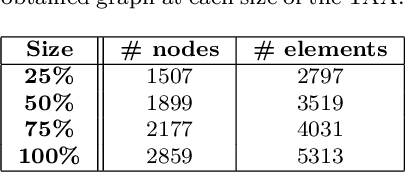
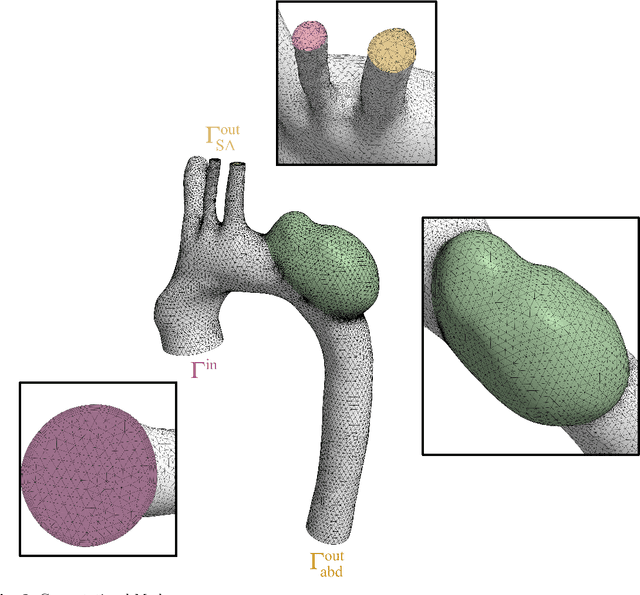
The complexity of the cardiovascular system needs to be accurately reproduced in order to promptly acknowledge health conditions; to this aim, advanced multifidelity and multiphysics numerical models are crucial. On one side, Full Order Models (FOMs) deliver accurate hemodynamic assessments, but their high computational demands hinder their real-time clinical application. In contrast, ROMs provide more efficient yet accurate solutions, essential for personalized healthcare and timely clinical decision-making. In this work, we explore the application of computational fluid dynamics (CFD) in cardiovascular medicine by integrating FOMs with ROMs for predicting the risk of aortic aneurysm growth and rupture. Wall Shear Stress (WSS) and the Oscillatory Shear Index (OSI), sampled at different growth stages of the abdominal aortic aneurysm, are predicted by means of Graph Neural Networks (GNNs). GNNs exploit the natural graph structure of the mesh obtained by the Finite Volume (FV) discretization, taking into account the spatial local information, regardless of the dimension of the input graph. Our experimental validation framework yields promising results, confirming our method as a valid alternative that overcomes the curse of dimensionality.

Extension of Recurrent Kernels to different Reservoir Computing topologies

Reservoir Computing (RC) has become popular in recent years due to its fast and efficient computational capabilities. Standard RC has been shown to be equivalent in the asymptotic limit to Recurrent Kernels, which helps in analyzing its expressive power. However, many well-established RC paradigms, such as Leaky RC, Sparse RC, and Deep RC, are yet to be analyzed in such a way. This study aims to fill this gap by providing an empirical analysis of the equivalence of specific RC architectures with their corresponding Recurrent Kernel formulation. We conduct a convergence study by varying the activation function implemented in each architecture. Our study also sheds light on the role of sparse connections in RC architectures and propose an optimal sparsity level that depends on the reservoir size. Furthermore, our systematic analysis shows that in Deep RC models, convergence is better achieved with successive reservoirs of decreasing sizes.

VC dimension of Graph Neural Networks with Pfaffian activation functions

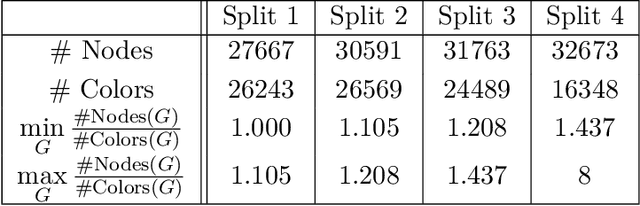
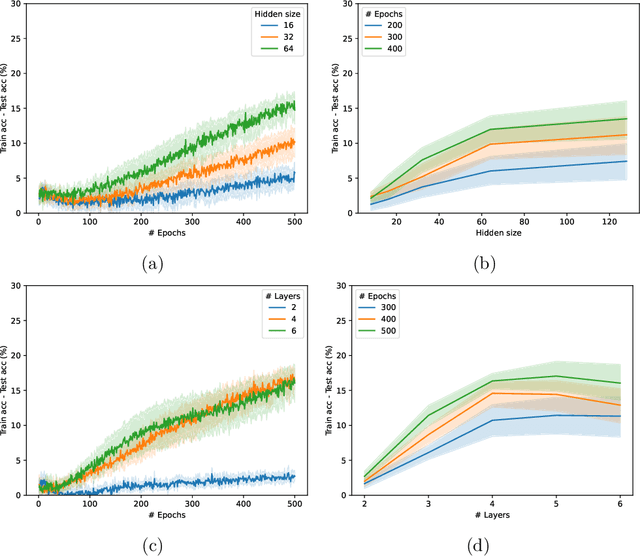
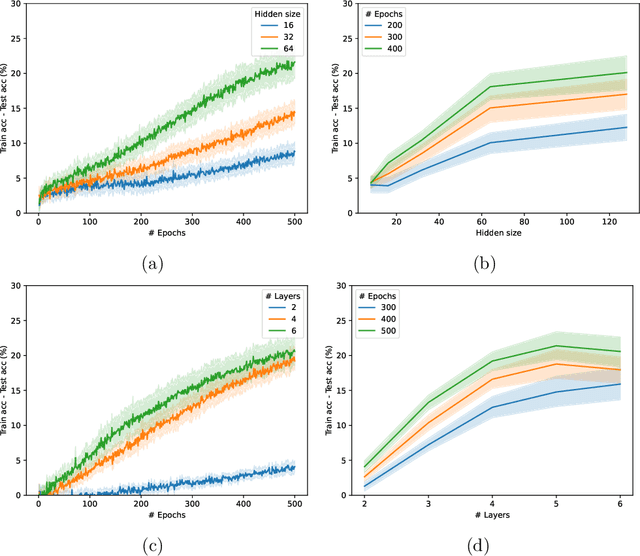
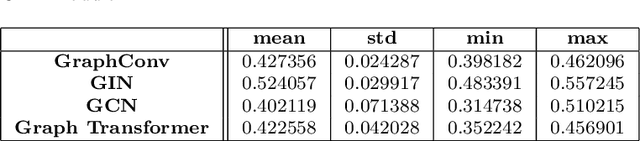
Graph Neural Networks (GNNs) have emerged in recent years as a powerful tool to learn tasks across a wide range of graph domains in a data-driven fashion; based on a message passing mechanism, GNNs have gained increasing popularity due to their intuitive formulation, closely linked with the Weisfeiler-Lehman (WL) test for graph isomorphism, to which they have proven equivalent. From a theoretical point of view, GNNs have been shown to be universal approximators, and their generalization capability (namely, bounds on the Vapnik Chervonekis (VC) dimension) has recently been investigated for GNNs with piecewise polynomial activation functions. The aim of our work is to extend this analysis on the VC dimension of GNNs to other commonly used activation functions, such as sigmoid and hyperbolic tangent, using the framework of Pfaffian function theory. Bounds are provided with respect to architecture parameters (depth, number of neurons, input size) as well as with respect to the number of colors resulting from the 1-WL test applied on the graph domain. The theoretical analysis is supported by a preliminary experimental study.

A topological description of loss surfaces based on Betti Numbers

In the context of deep learning models, attention has recently been paid to studying the surface of the loss function in order to better understand training with methods based on gradient descent. This search for an appropriate description, both analytical and topological, has led to numerous efforts to identify spurious minima and characterize gradient dynamics. Our work aims to contribute to this field by providing a topological measure to evaluate loss complexity in the case of multilayer neural networks. We compare deep and shallow architectures with common sigmoidal activation functions by deriving upper and lower bounds on the complexity of their loss function and revealing how that complexity is influenced by the number of hidden units, training models, and the activation function used. Additionally, we found that certain variations in the loss function or model architecture, such as adding an $\ell_2$ regularization term or implementing skip connections in a feedforward network, do not affect loss topology in specific cases.

Generalization Limits of Graph Neural Networks in Identity Effects Learning

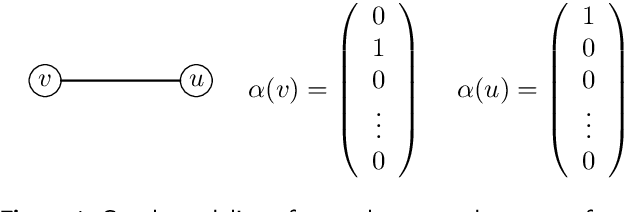
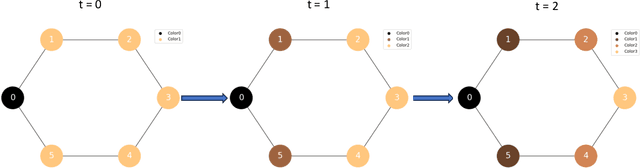
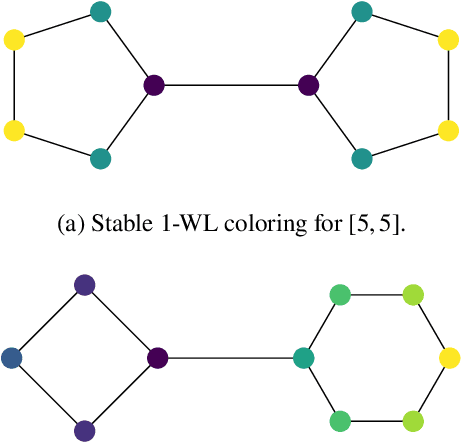
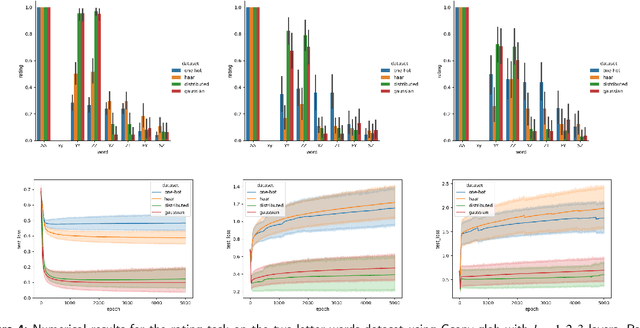
Graph Neural Networks (GNNs) have emerged as a powerful tool for data-driven learning on various graph domains. They are usually based on a message-passing mechanism and have gained increasing popularity for their intuitive formulation, which is closely linked to the Weisfeiler-Lehman (WL) test for graph isomorphism to which they have been proven equivalent in terms of expressive power. In this work, we establish new generalization properties and fundamental limits of GNNs in the context of learning so-called identity effects, i.e., the task of determining whether an object is composed of two identical components or not. Our study is motivated by the need to understand the capabilities of GNNs when performing simple cognitive tasks, with potential applications in computational linguistics and chemistry. We analyze two case studies: (i) two-letters words, for which we show that GNNs trained via stochastic gradient descent are unable to generalize to unseen letters when utilizing orthogonal encodings like one-hot representations; (ii) dicyclic graphs, i.e., graphs composed of two cycles, for which we present positive existence results leveraging the connection between GNNs and the WL test. Our theoretical analysis is supported by an extensive numerical study.

Weisfeiler--Lehman goes Dynamic: An Analysis of the Expressive Power of Graph Neural Networks for Attributed and Dynamic Graphs

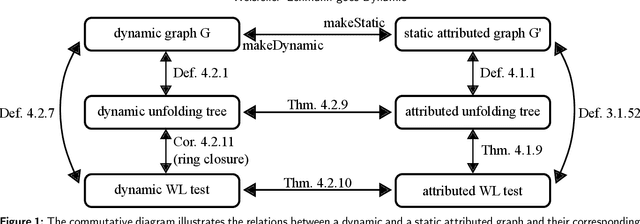
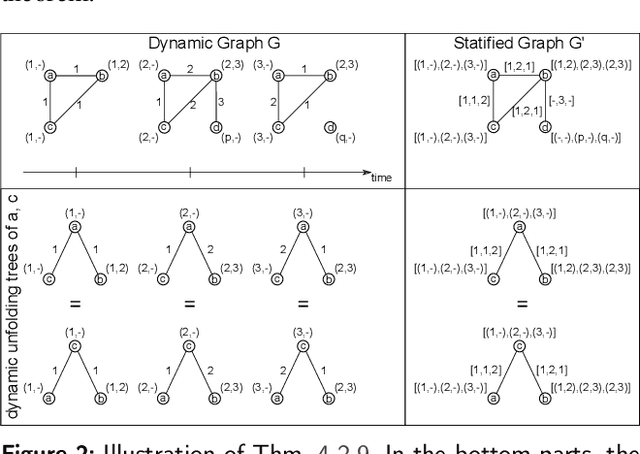
Graph Neural Networks (GNNs) are a large class of relational models for graph processing. Recent theoretical studies on the expressive power of GNNs have focused on two issues. On the one hand, it has been proven that GNNs are as powerful as the Weisfeiler-Lehman test (1-WL) in their ability to distinguish graphs. Moreover, it has been shown that the equivalence enforced by 1-WL equals unfolding equivalence. On the other hand, GNNs turned out to be universal approximators on graphs modulo the constraints enforced by 1-WL/unfolding equivalence. However, these results only apply to Static Undirected Homogeneous Graphs with node attributes. In contrast, real-life applications often involve a variety of graph properties, such as, e.g., dynamics or node and edge attributes. In this paper, we conduct a theoretical analysis of the expressive power of GNNs for these two graph types that are particularly of interest. Dynamic graphs are widely used in modern applications, and its theoretical analysis requires new approaches. The attributed type acts as a standard form for all graph types since it has been shown that all graph types can be transformed without loss to Static Undirected Homogeneous Graphs with attributes on nodes and edges (SAUHG). The study considers generic GNN models and proposes appropriate 1-WL tests for those domains. Then, the results on the expressive power of GNNs are extended by proving that GNNs have the same capability as the 1-WL test in distinguishing dynamic and attributed graphs, the 1-WL equivalence equals unfolding equivalence and that GNNs are universal approximators modulo 1-WL/unfolding equivalence. Moreover, the proof of the approximation capability holds for SAUHGs, which include most of those used in practical applications, and it is constructive in nature allowing to deduce hints on the architecture of GNNs that can achieve the desired accuracy.

A unifying point of view on expressive power of GNNs

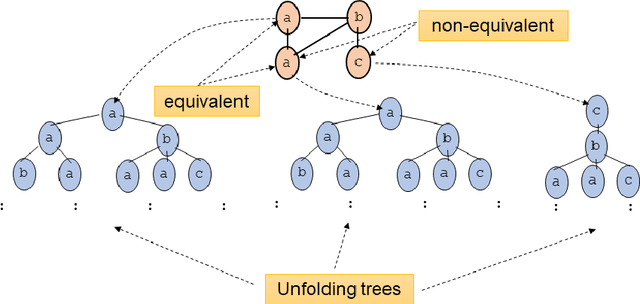
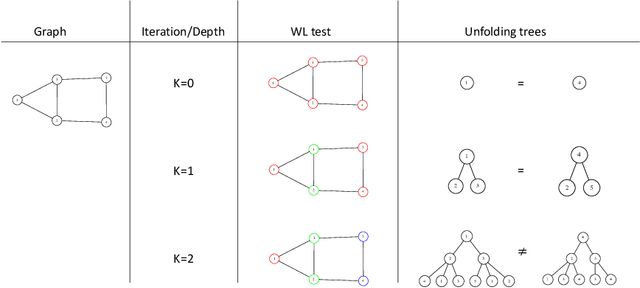
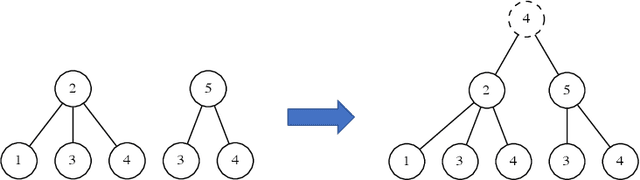
Graph Neural Networks (GNNs) are a wide class of connectionist models for graph processing. They perform an iterative message passing operation on each node and its neighbors, to solve classification/ clustering tasks -- on some nodes or on the whole graph -- collecting all such messages, regardless of their order. Despite the differences among the various models belonging to this class, most of them adopt the same computation scheme, based on a local aggregation mechanism and, intuitively, the local computation framework is mainly responsible for the expressive power of GNNs. In this paper, we prove that the Weisfeiler--Lehman test induces an equivalence relationship on the graph nodes that exactly corresponds to the unfolding equivalence, defined on the original GNN model. Therefore, the results on the expressive power of the original GNNs can be extended to general GNNs which, under mild conditions, can be proved capable of approximating, in probability and up to any precision, any function on graphs that respects the unfolding equivalence.