Generalization Limits of Graph Neural Networks in Identity Effects Learning
Paper and Code
Jun 30, 2023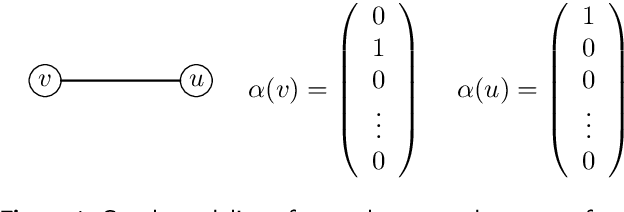
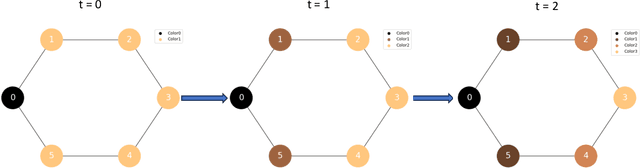
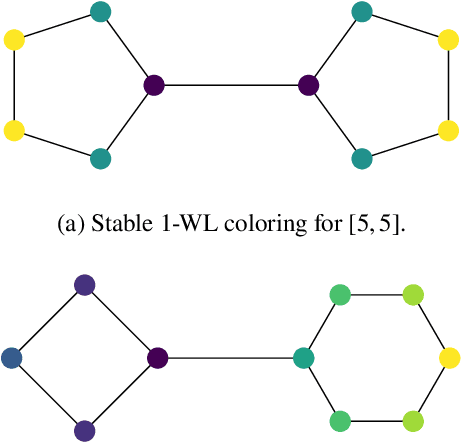
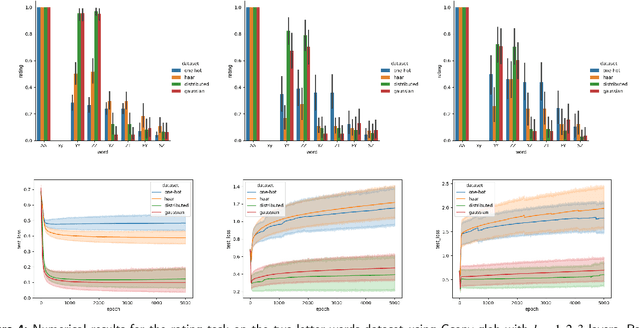
Graph Neural Networks (GNNs) have emerged as a powerful tool for data-driven learning on various graph domains. They are usually based on a message-passing mechanism and have gained increasing popularity for their intuitive formulation, which is closely linked to the Weisfeiler-Lehman (WL) test for graph isomorphism to which they have been proven equivalent in terms of expressive power. In this work, we establish new generalization properties and fundamental limits of GNNs in the context of learning so-called identity effects, i.e., the task of determining whether an object is composed of two identical components or not. Our study is motivated by the need to understand the capabilities of GNNs when performing simple cognitive tasks, with potential applications in computational linguistics and chemistry. We analyze two case studies: (i) two-letters words, for which we show that GNNs trained via stochastic gradient descent are unable to generalize to unseen letters when utilizing orthogonal encodings like one-hot representations; (ii) dicyclic graphs, i.e., graphs composed of two cycles, for which we present positive existence results leveraging the connection between GNNs and the WL test. Our theoretical analysis is supported by an extensive numerical study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge