Damien Briens
Physics-Informed GNN for non-linear constrained optimization: PINCO a solver for the AC-optimal power flow
Oct 07, 2024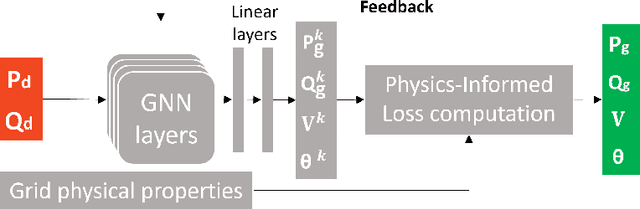

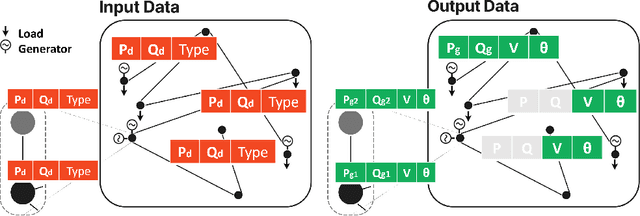

Abstract:The energy transition is driving the integration of large shares of intermittent power sources in the electric power grid. Therefore, addressing the AC optimal power flow (AC-OPF) effectively becomes increasingly essential. The AC-OPF, which is a fundamental optimization problem in power systems, must be solved more frequently to ensure the safe and cost-effective operation of power systems. Due to its non-linear nature, AC-OPF is often solved in its linearized form, despite inherent inaccuracies. Non-linear solvers, such as the interior point method, are typically employed to solve the full OPF problem. However, these iterative methods may not converge for large systems and do not guarantee global optimality. This work explores a physics-informed graph neural network, PINCO, to solve the AC-OPF. We demonstrate that this method provides accurate solutions in a fraction of the computational time when compared to the established non-linear programming solvers. Remarkably, PINCO generalizes effectively across a diverse set of loading conditions in the power system. We show that our method can solve the AC-OPF without violating inequality constraints. Furthermore, it can function both as a solver and as a hybrid universal function approximator. Moreover, the approach can be easily adapted to different power systems with minimal adjustments to the hyperparameters, including systems with multiple generators at each bus. Overall, this work demonstrates an advancement in the field of power system optimization to tackle the challenges of the energy transition. The code and data utilized in this paper are available at https://anonymous.4open.science/r/opf_pinn_iclr-B83E/.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge