Physics-Informed GNN for non-linear constrained optimization: PINCO a solver for the AC-optimal power flow

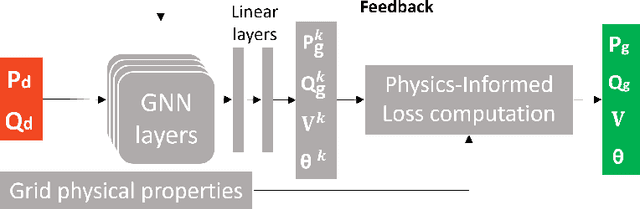
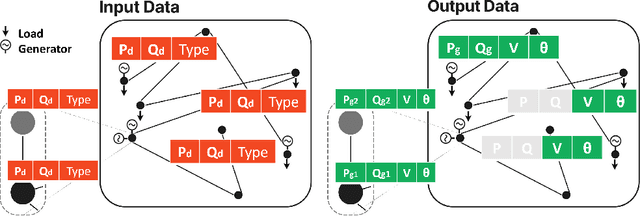
The energy transition is driving the integration of large shares of intermittent power sources in the electric power grid. Therefore, addressing the AC optimal power flow (AC-OPF) effectively becomes increasingly essential. The AC-OPF, which is a fundamental optimization problem in power systems, must be solved more frequently to ensure the safe and cost-effective operation of power systems. Due to its non-linear nature, AC-OPF is often solved in its linearized form, despite inherent inaccuracies. Non-linear solvers, such as the interior point method, are typically employed to solve the full OPF problem. However, these iterative methods may not converge for large systems and do not guarantee global optimality. This work explores a physics-informed graph neural network, PINCO, to solve the AC-OPF. We demonstrate that this method provides accurate solutions in a fraction of the computational time when compared to the established non-linear programming solvers. Remarkably, PINCO generalizes effectively across a diverse set of loading conditions in the power system. We show that our method can solve the AC-OPF without violating inequality constraints. Furthermore, it can function both as a solver and as a hybrid universal function approximator. Moreover, the approach can be easily adapted to different power systems with minimal adjustments to the hyperparameters, including systems with multiple generators at each bus. Overall, this work demonstrates an advancement in the field of power system optimization to tackle the challenges of the energy transition. The code and data utilized in this paper are available at https://anonymous.4open.science/r/opf_pinn_iclr-B83E/.

A Perspective on Foundation Models for the Electric Power Grid

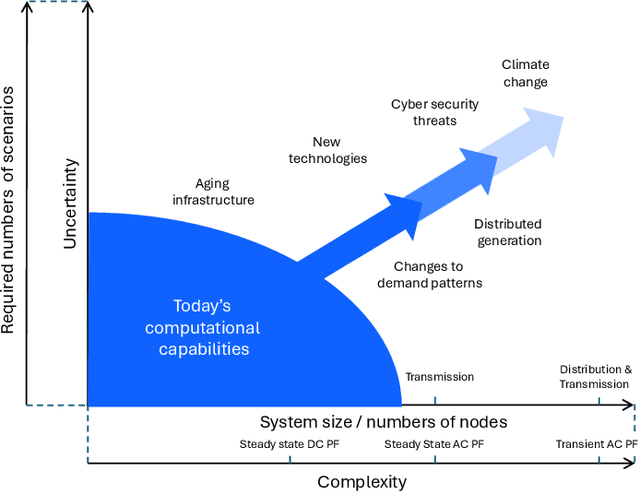
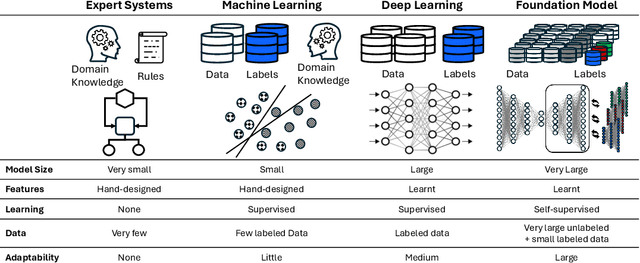
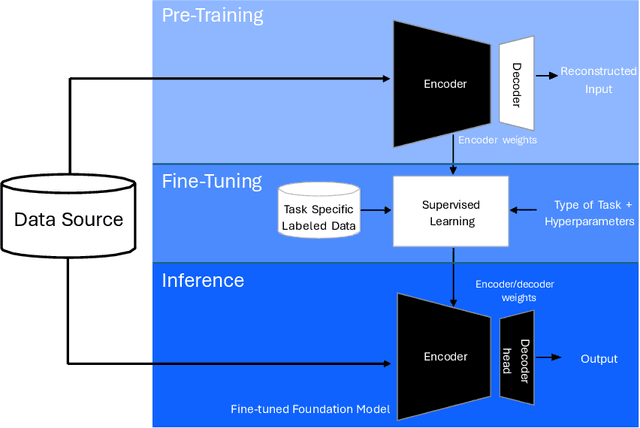
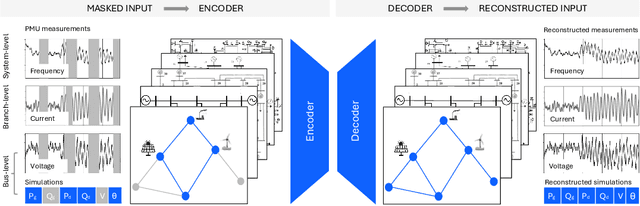
Foundation models (FMs) currently dominate news headlines. They employ advanced deep learning architectures to extract structural information autonomously from vast datasets through self-supervision. The resulting rich representations of complex systems and dynamics can be applied to many downstream applications. Therefore, FMs can find uses in electric power grids, challenged by the energy transition and climate change. In this paper, we call for the development of, and state why we believe in, the potential of FMs for electric grids. We highlight their strengths and weaknesses amidst the challenges of a changing grid. We argue that an FM learning from diverse grid data and topologies could unlock transformative capabilities, pioneering a new approach in leveraging AI to redefine how we manage complexity and uncertainty in the electric grid. Finally, we discuss a power grid FM concept, namely GridFM, based on graph neural networks and show how different downstream tasks benefit.

PowerGraph: A power grid benchmark dataset for graph neural networks

Public Graph Neural Networks (GNN) benchmark datasets facilitate the use of GNN and enhance GNN applicability to diverse disciplines. The community currently lacks public datasets of electrical power grids for GNN applications. Indeed, GNNs can potentially capture complex power grid phenomena over alternative machine learning techniques. Power grids are complex engineered networks that are naturally amenable to graph representations. Therefore, GNN have the potential for capturing the behavior of power grids over alternative machine learning techniques. To this aim, we develop a graph dataset for cascading failure events, which are the major cause of blackouts in electric power grids. Historical blackout datasets are scarce and incomplete. The assessment of vulnerability and the identification of critical components are usually conducted via computationally expensive offline simulations of cascading failures. Instead, we propose using machine learning models for the online detection of cascading failures leveraging the knowledge of the system state at the onset of the cascade. We develop PowerGraph, a graph dataset modeling cascading failures in power grids, designed for two purposes, namely, i) training GNN models for different graph-level tasks including multi-class classification, binary classification, and regression, and ii) explaining GNN models. The dataset generated via a physics-based cascading failure model ensures the generality of the operating and environmental conditions by spanning diverse failure scenarios. In addition, we foster the use of the dataset to benchmark GNN explainability methods by assigning ground-truth edge-level explanations. PowerGraph helps the development of better GNN models for graph-level tasks and explainability, critical in many domains ranging from chemistry to biology, where the systems and processes can be described as graphs.