Sparsely Pre-transformed Polar Codes for Low-Latency SCL Decoding

Deep polar codes, employing multi-layered polar kernel pre-transforms in series, are recently introduced variants of pre-transformed polar codes. These codes have demonstrated the ability to reduce the number of minimum weight codewords, thereby closely achieving finite-block length capacity with successive cancellation list (SCL) decoders in certain scenarios. However, when the list size of the SCL decoder is small, which is crucial for low-latency communication applications, the reduction in the number of minimum weight codewords does not necessarily improve decoding performance. To address this limitation, we propose an alternative pre-transform technique to enhance the suitability of polar codes for SCL decoders with practical list sizes. Leveraging the fact that the SCL decoding error event set can be decomposed into two exclusive error event sets, our approach applies two different types of pre-transformations, each targeting the reduction of one of the two error event sets. Extensive simulation results under various block lengths and code rates have demonstrated that our codes consistently outperform all existing state-of-the-art pre-transformed polar codes, including CRC-aided polar codes and polarization-adjusted convolutional codes, when decoded using SCL decoders with small list sizes.

Nonlinear Self-Interference Cancellation With Learnable Orthonormal Polynomials for Full-Duplex Wireless Systems

Nonlinear self-interference cancellation (SIC) is essential for full-duplex communication systems, which can offer twice the spectral efficiency of traditional half-duplex systems. The challenge of nonlinear SIC is similar to the classic problem of system identification in adaptive filter theory, whose crux lies in identifying the optimal nonlinear basis functions for a nonlinear system. This becomes especially difficult when the system input has a non-stationary distribution. In this paper, we propose a novel algorithm for nonlinear digital SIC that adaptively constructs orthonormal polynomial basis functions according to the non-stationary moments of the transmit signal. By combining these basis functions with the least mean squares (LMS) algorithm, we introduce a new SIC technique, called as the adaptive orthonormal polynomial LMS (AOP-LMS) algorithm. To reduce computational complexity for practical systems, we augment our approach with a precomputed look-up table, which maps a given modulation and coding scheme to its corresponding basis functions. Numerical simulation indicates that our proposed method surpasses existing state-of-the-art SIC algorithms in terms of convergence speed and mean squared error when the transmit signal is non-stationary, such as with adaptive modulation and coding. Experimental evaluation with a wireless testbed confirms that our proposed approach outperforms existing digital SIC algorithms.

Deep Polar Codes

In this paper, we introduce a novel class of pre-transformed polar codes, termed as deep polar codes. We first present a deep polar encoder that harnesses a series of multi-layered polar transformations with varying sizes. Our approach to encoding enables a low-complexity implementation while significantly enhancing the weight distribution of the code. Moreover, our encoding method offers flexibility in rate-profiling, embracing a wide range of code rates and blocklengths. Next, we put forth a low-complexity decoding algorithm called successive cancellation list with backpropagation parity checks (SCL-BPC). This decoding algorithm leverages the parity check equations in the reverse process of the multi-layered pre-transformed encoding for SCL decoding. Additionally, we present a low-latency decoding algorithm that employs parallel-SCL decoding by treating partially pre-transformed bit patterns as additional frozen bits. Through simulations, we demonstrate that deep polar codes outperform existing pre-transformed polar codes in terms of block error rates across various code rates under short block lengths, while maintaining low encoding and decoding complexity. Furthermore, we show that concatenating deep polar codes with cyclic-redundancy-check codes can achieve the meta-converse bound of the finite block length capacity within 0.4 dB in some instances.

Information-Theoretical Approach to Integrated Pulse-Doppler Radar and Communication Systems

Integrated sensing and communication improves the design of systems by combining sensing and communication functions for increased efficiency, accuracy, and cost savings. The optimal integration requires understanding the trade-off between sensing and communication, but this can be difficult due to the lack of unified performance metrics. In this paper, an information-theoretical approach is used to design the system with a unified metric. A sensing rate is introduced to measure the amount of information obtained by a pulse-Doppler radar system. An approximation and lower bound of the sensing rate is obtained in closed forms. Using both the derived sensing information and communication rates, the optimal bandwidth allocation strategy is found for maximizing the weighted sum of the spectral efficiency for sensing and communication. The simulation results confirm the validity of the approximation and the effectiveness of the proposed bandwidth allocation.

Split-KalmanNet: A Robust Model-Based Deep Learning Approach for SLAM

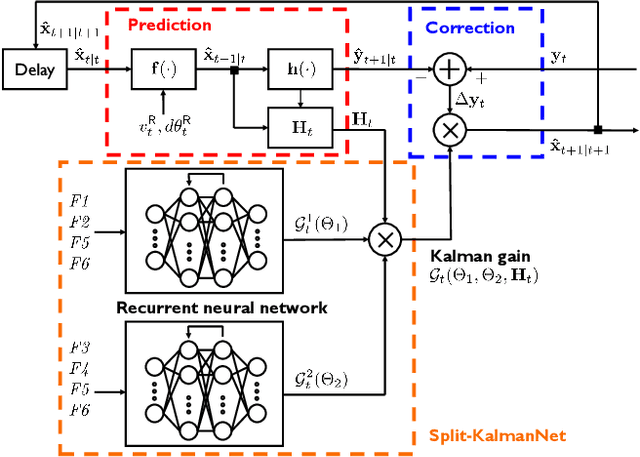
Simultaneous localization and mapping (SLAM) is a method that constructs a map of an unknown environment and localizes the position of a moving agent on the map simultaneously. Extended Kalman filter (EKF) has been widely adopted as a low complexity solution for online SLAM, which relies on a motion and measurement model of the moving agent. In practice, however, acquiring precise information about these models is very challenging, and the model mismatch effect causes severe performance loss in SLAM. In this paper, inspired by the recently proposed KalmanNet, we present a robust EKF algorithm using the power of deep learning for online SLAM, referred to as Split-KalmanNet. The key idea of Split-KalmanNet is to compute the Kalman gain using the Jacobian matrix of a measurement function and two recurrent neural networks (RNNs). The two RNNs independently learn the covariance matrices for a prior state estimate and the innovation from data. The proposed split structure in the computation of the Kalman gain allows to compensate for state and measurement model mismatch effects independently. Numerical simulation results verify that Split-KalmanNet outperforms the traditional EKF and the state-of-the-art KalmanNet algorithm in various model mismatch scenarios.