Signature Isolation Forest

Functional Isolation Forest (FIF) is a recent state-of-the-art Anomaly Detection (AD) algorithm designed for functional data. It relies on a tree partition procedure where an abnormality score is computed by projecting each curve observation on a drawn dictionary through a linear inner product. Such linear inner product and the dictionary are a priori choices that highly influence the algorithm's performances and might lead to unreliable results, particularly with complex datasets. This work addresses these challenges by introducing \textit{Signature Isolation Forest}, a novel AD algorithm class leveraging the rough path theory's signature transform. Our objective is to remove the constraints imposed by FIF through the proposition of two algorithms which specifically target the linearity of the FIF inner product and the choice of the dictionary. We provide several numerical experiments, including a real-world applications benchmark showing the relevance of our methods.

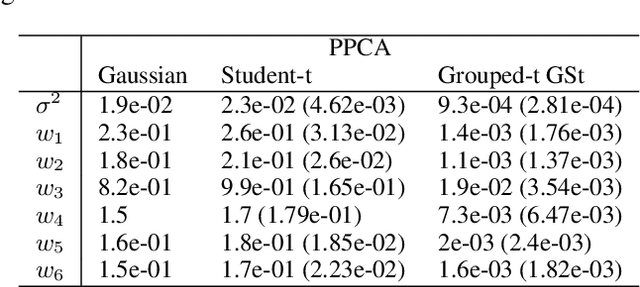
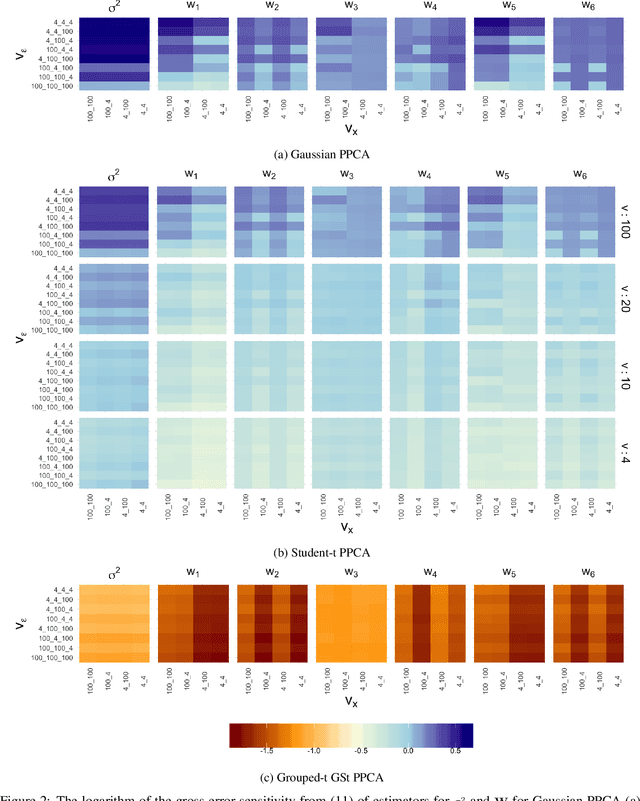
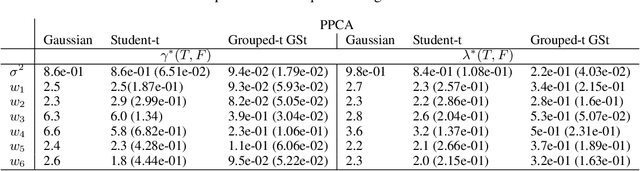
Parsimonious Feature Extraction Methods: Extending Robust Probabilistic Projections with Generalized Skew-t

We propose a novel generalisation to the Student-t Probabilistic Principal Component methodology which: (1) accounts for an asymmetric distribution of the observation data; (2) is a framework for grouped and generalised multiple-degree-of-freedom structures, which provides a more flexible approach to modelling groups of marginal tail dependence in the observation data; and (3) separates the tail effect of the error terms and factors. The new feature extraction methods are derived in an incomplete data setting to efficiently handle the presence of missing values in the observation vector. We discuss various special cases of the algorithm being a result of simplified assumptions on the process generating the data. The applicability of the new framework is illustrated on a data set that consists of crypto currencies with the highest market capitalisation.

Cost-aware Feature Selection for IoT Device Classification

Classification of IoT devices into different types is of paramount importance, from multiple perspectives, including security and privacy aspects. Recent works have explored machine learning techniques for fingerprinting (or classifying) IoT devices, with promising results. However, existing works have assumed that the features used for building the machine learning models are readily available or can be easily extracted from the network traffic; in other words, they do not consider the costs associated with feature extraction. In this work, we take a more realistic approach, and argue that feature extraction has a cost, and the costs are different for different features. We also take a step forward from the current practice of considering the misclassification loss as a binary value, and make a case for different losses based on the misclassification performance. Thereby, and more importantly, we introduce the notion of risk for IoT device classification. We define and formulate the problem of cost-aware IoT device classification. This being a combinatorial optimization problem, we develop a novel algorithm to solve it in a fast and effective way using the Cross-Entropy (CE) based stochastic optimization technique. Using traffic of real devices, we demonstrate the capability of the CE based algorithm in selecting features with minimal risk of misclassification while keeping the cost for feature extraction within a specified limit.

Sensor Selection and Random Field Reconstruction for Robust and Cost-effective Heterogeneous Weather Sensor Networks for the Developing World

We address the two fundamental problems of spatial field reconstruction and sensor selection in heterogeneous sensor networks: (i) how to efficiently perform spatial field reconstruction based on measurements obtained simultaneously from networks with both high and low quality sensors; and (ii) how to perform query based sensor set selection with predictive MSE performance guarantee. For the first problem, we developed a low complexity algorithm based on the spatial best linear unbiased estimator (S-BLUE). Next, building on the S-BLUE, we address the second problem, and develop an efficient algorithm for query based sensor set selection with performance guarantee. Our algorithm is based on the Cross Entropy method which solves the combinatorial optimization problem in an efficient manner.

Riemannian tangent space mapping and elastic net regularization for cost-effective EEG markers of brain atrophy in Alzheimer's disease

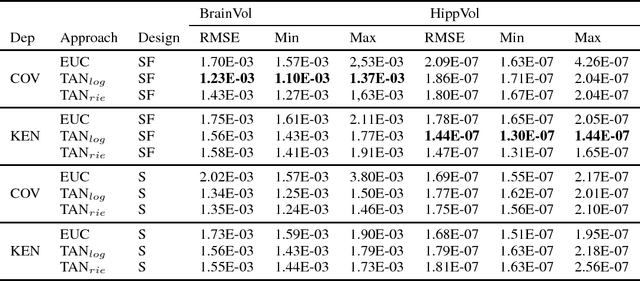
The diagnosis of Alzheimer's disease (AD) in routine clinical practice is most commonly based on subjective clinical interpretations. Quantitative electroencephalography (QEEG) measures have been shown to reflect neurodegenerative processes in AD and might qualify as affordable and thereby widely available markers to facilitate the objectivization of AD assessment. Here, we present a novel framework combining Riemannian tangent space mapping and elastic net regression for the development of brain atrophy markers. While most AD QEEG studies are based on small sample sizes and psychological test scores as outcome measures, here we train and test our models using data of one of the largest prospective EEG AD trials ever conducted, including MRI biomarkers of brain atrophy.

Discussion of "Riemann manifold Langevin and Hamiltonian Monte Carlo methods'' by M. Girolami and B. Calderhead

This technical report is the union of two contributions to the discussion of the Read Paper "Riemann manifold Langevin and Hamiltonian Monte Carlo methods" by B. Calderhead and M. Girolami, presented in front of the Royal Statistical Society on October 13th 2010 and to appear in the Journal of the Royal Statistical Society Series B. The first comment establishes a parallel and possible interactions with Adaptive Monte Carlo methods. The second comment exposes a detailed study of Riemannian Manifold Hamiltonian Monte Carlo (RMHMC) for a weakly identifiable model presenting a strong ridge in its geometry.

Ecological non-linear state space model selection via adaptive particle Markov chain Monte Carlo (AdPMCMC)

We develop a novel advanced Particle Markov chain Monte Carlo algorithm that is capable of sampling from the posterior distribution of non-linear state space models for both the unobserved latent states and the unknown model parameters. We apply this novel methodology to five population growth models, including models with strong and weak Allee effects, and test if it can efficiently sample from the complex likelihood surface that is often associated with these models. Utilising real and also synthetically generated data sets we examine the extent to which observation noise and process error may frustrate efforts to choose between these models. Our novel algorithm involves an Adaptive Metropolis proposal combined with an SIR Particle MCMC algorithm (AdPMCMC). We show that the AdPMCMC algorithm samples complex, high-dimensional spaces efficiently, and is therefore superior to standard Gibbs or Metropolis Hastings algorithms that are known to converge very slowly when applied to the non-linear state space ecological models considered in this paper. Additionally, we show how the AdPMCMC algorithm can be used to recursively estimate the Bayesian Cram\'er-Rao Lower Bound of Tichavsk\'y (1998). We derive expressions for these Cram\'er-Rao Bounds and estimate them for the models considered. Our results demonstrate a number of important features of common population growth models, most notably their multi-modal posterior surfaces and dependence between the static and dynamic parameters. We conclude by sampling from the posterior distribution of each of the models, and use Bayes factors to highlight how observation noise significantly diminishes our ability to select among some of the models, particularly those that are designed to reproduce an Allee effect.