Computing the Newton-step faster than Hessian accumulation

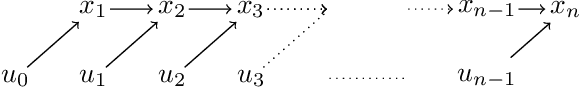
Computing the Newton-step of a generic function with $N$ decision variables takes $O(N^3)$ flops. In this paper, we show that given the computational graph of the function, this bound can be reduced to $O(m\tau^3)$, where $\tau, m$ are the width and size of a tree-decomposition of the graph. The proposed algorithm generalizes nonlinear optimal-control methods based on LQR to general optimization problems and provides non-trivial gains in iteration-complexity even in cases where the Hessian is dense.

Lyceum: An efficient and scalable ecosystem for robot learning

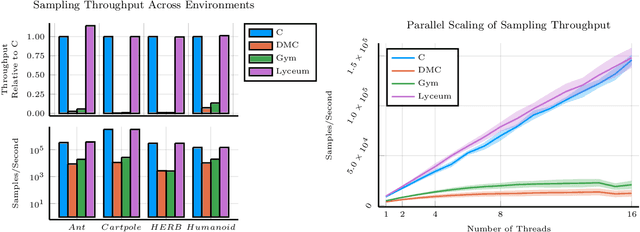
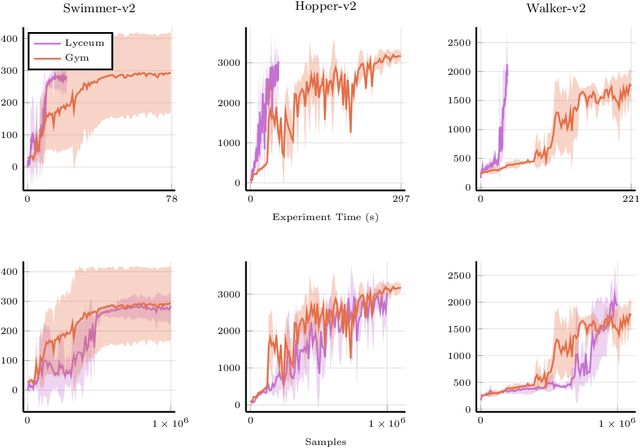
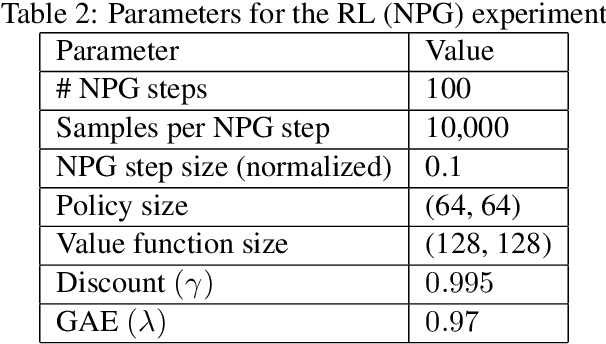
We introduce Lyceum, a high-performance computational ecosystem for robot learning. Lyceum is built on top of the Julia programming language and the MuJoCo physics simulator, combining the ease-of-use of a high-level programming language with the performance of native C. In addition, Lyceum has a straightforward API to support parallel computation across multiple cores and machines. Overall, depending on the complexity of the environment, Lyceum is 5-30x faster compared to other popular abstractions like OpenAI's Gym and DeepMind's dm-control. This substantially reduces training time for various reinforcement learning algorithms; and is also fast enough to support real-time model predictive control through MuJoCo. The code, tutorials, and demonstration videos can be found at: www.lyceum.ml.

Plan Online, Learn Offline: Efficient Learning and Exploration via Model-Based Control

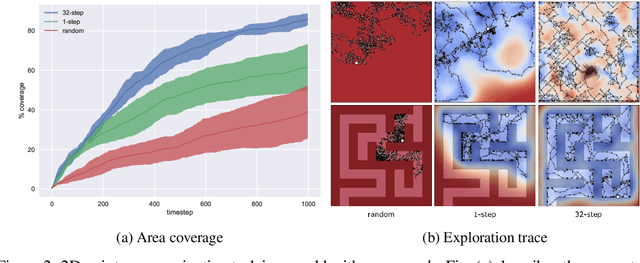
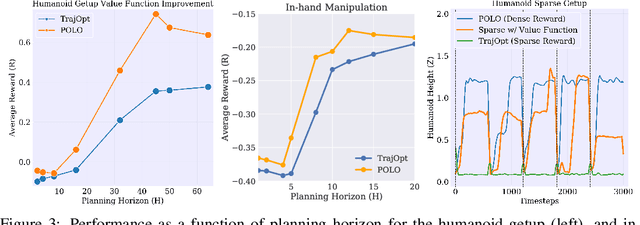
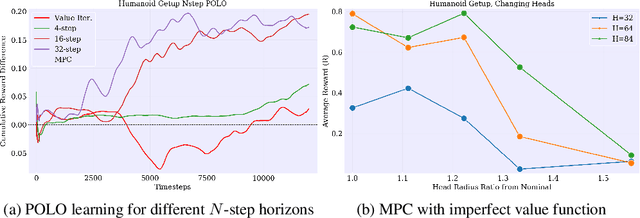
We propose a plan online and learn offline (POLO) framework for the setting where an agent, with an internal model, needs to continually act and learn in the world. Our work builds on the synergistic relationship between local model-based control, global value function learning, and exploration. We study how local trajectory optimization can cope with approximation errors in the value function, and can stabilize and accelerate value function learning. Conversely, we also study how approximate value functions can help reduce the planning horizon and allow for better policies beyond local solutions. Finally, we also demonstrate how trajectory optimization can be used to perform temporally coordinated exploration in conjunction with estimating uncertainty in value function approximation. This exploration is critical for fast and stable learning of the value function. Combining these components enable solutions to complex simulated control tasks, like humanoid locomotion and dexterous in-hand manipulation, in the equivalent of a few minutes of experience in the real world.

Learning Complex Dexterous Manipulation with Deep Reinforcement Learning and Demonstrations

Dexterous multi-fingered hands are extremely versatile and provide a generic way to perform a multitude of tasks in human-centric environments. However, effectively controlling them remains challenging due to their high dimensionality and large number of potential contacts. Deep reinforcement learning (DRL) provides a model-agnostic approach to control complex dynamical systems, but has not been shown to scale to high-dimensional dexterous manipulation. Furthermore, deployment of DRL on physical systems remains challenging due to sample inefficiency. Consequently, the success of DRL in robotics has thus far been limited to simpler manipulators and tasks. In this work, we show that model-free DRL can effectively scale up to complex manipulation tasks with a high-dimensional 24-DoF hand, and solve them from scratch in simulated experiments. Furthermore, with the use of a small number of human demonstrations, the sample complexity can be significantly reduced, which enables learning with sample sizes equivalent to a few hours of robot experience. The use of demonstrations result in policies that exhibit very natural movements and, surprisingly, are also substantially more robust.

Reinforcement learning for non-prehensile manipulation: Transfer from simulation to physical system

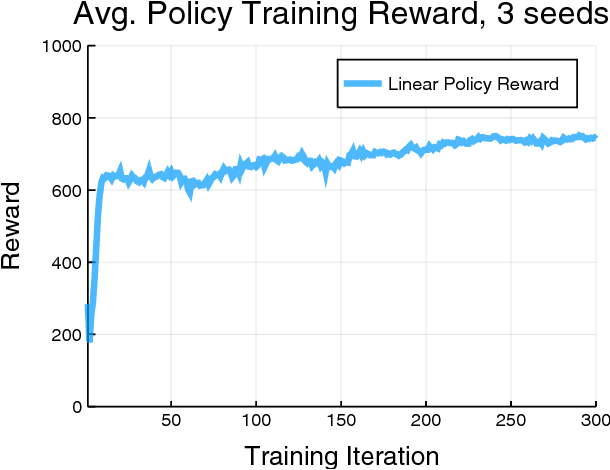
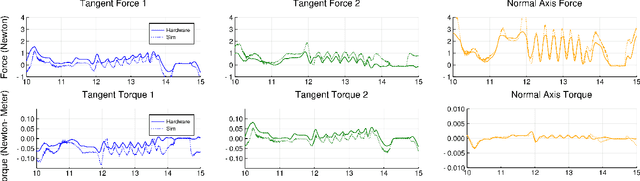
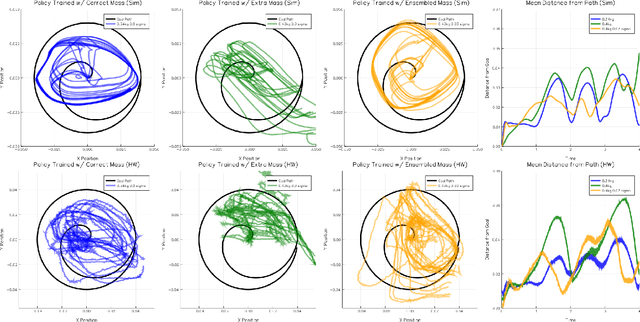
Reinforcement learning has emerged as a promising methodology for training robot controllers. However, most results have been limited to simulation due to the need for a large number of samples and the lack of automated-yet-safe data collection methods. Model-based reinforcement learning methods provide an avenue to circumvent these challenges, but the traditional concern has been the mismatch between the simulator and the real world. Here, we show that control policies learned in simulation can successfully transfer to a physical system, composed of three Phantom robots pushing an object to various desired target positions. We use a modified form of the natural policy gradient algorithm for learning, applied to a carefully identified simulation model. The resulting policies, trained entirely in simulation, work well on the physical system without additional training. In addition, we show that training with an ensemble of models makes the learned policies more robust to modeling errors, thus compensating for difficulties in system identification.

Towards Generalization and Simplicity in Continuous Control

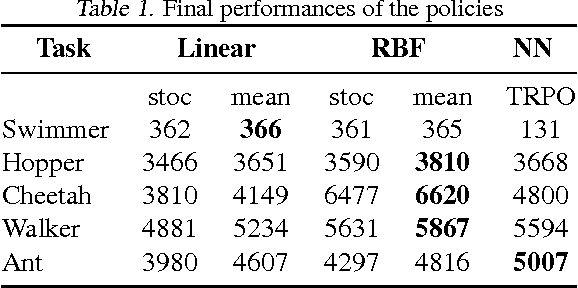
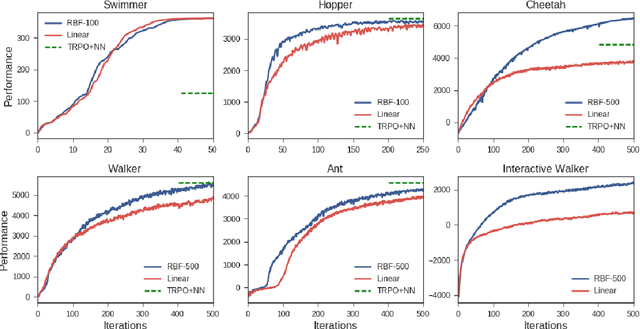
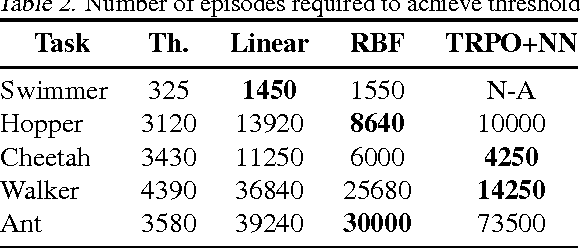
This work shows that policies with simple linear and RBF parameterizations can be trained to solve a variety of continuous control tasks, including the OpenAI gym benchmarks. The performance of these trained policies are competitive with state of the art results, obtained with more elaborate parameterizations such as fully connected neural networks. Furthermore, existing training and testing scenarios are shown to be very limited and prone to over-fitting, thus giving rise to only trajectory-centric policies. Training with a diverse initial state distribution is shown to produce more global policies with better generalization. This allows for interactive control scenarios where the system recovers from large on-line perturbations; as shown in the supplementary video.

Graphical Newton

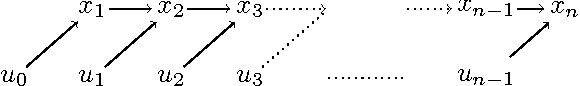
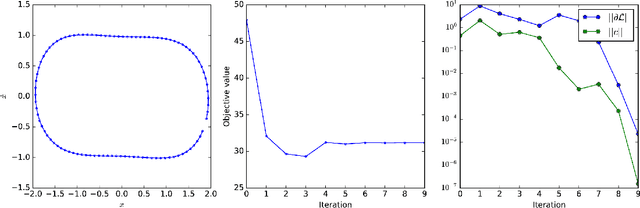
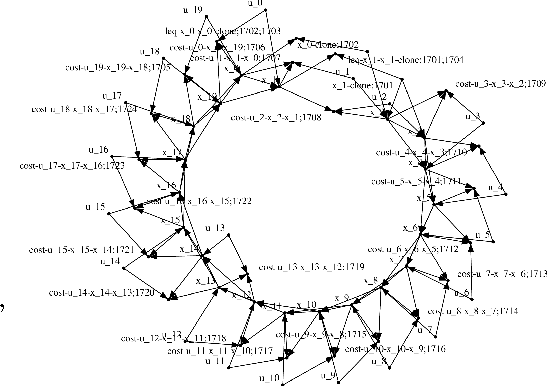
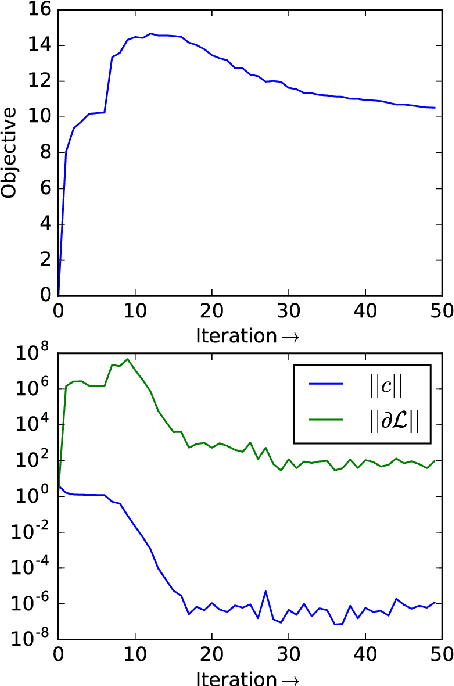
Computing the Newton step for a generic function $f: \mathbb{R}^N \rightarrow \mathbb{R}$ takes $O(N^{3})$ flops. In this paper, we explore avenues for reducing this bound, when the computational structure of $f$ is known beforehand. It is shown that the Newton step can be computed in time, linear in the size of the computational-graph, and cubic in its tree-width.

Learning Dexterous Manipulation Policies from Experience and Imitation

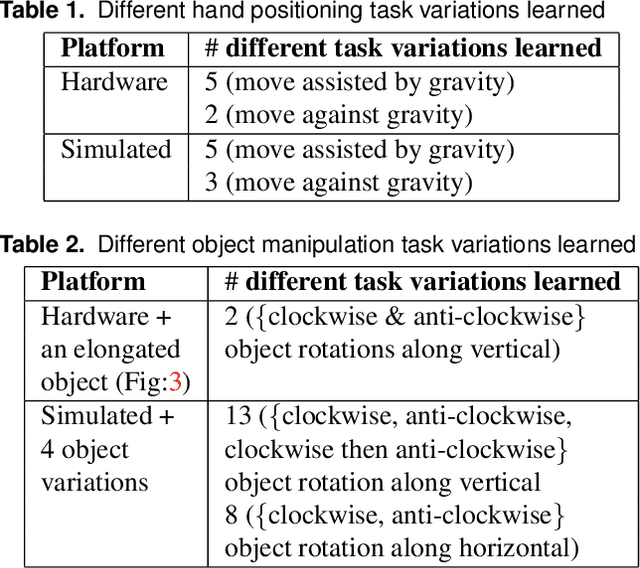
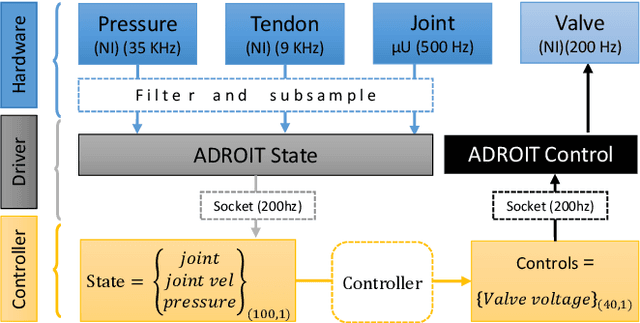
We explore learning-based approaches for feedback control of a dexterous five-finger hand performing non-prehensile manipulation. First, we learn local controllers that are able to perform the task starting at a predefined initial state. These controllers are constructed using trajectory optimization with respect to locally-linear time-varying models learned directly from sensor data. In some cases, we initialize the optimizer with human demonstrations collected via teleoperation in a virtual environment. We demonstrate that such controllers can perform the task robustly, both in simulation and on the physical platform, for a limited range of initial conditions around the trained starting state. We then consider two interpolation methods for generalizing to a wider range of initial conditions: deep learning, and nearest neighbors. We find that nearest neighbors achieve higher performance. Nevertheless, the neural network has its advantages: it uses only tactile and proprioceptive feedback but no visual feedback about the object (i.e. it performs the task blind) and learns a time-invariant policy. In contrast, the nearest neighbors method switches between time-varying local controllers based on the proximity of initial object states sensed via motion capture. While both generalization methods leave room for improvement, our work shows that (i) local trajectory-based controllers for complex non-prehensile manipulation tasks can be constructed from surprisingly small amounts of training data, and (ii) collections of such controllers can be interpolated to form more global controllers. Results are summarized in the supplementary video: https://youtu.be/E0wmO6deqjo

Universal Convexification via Risk-Aversion

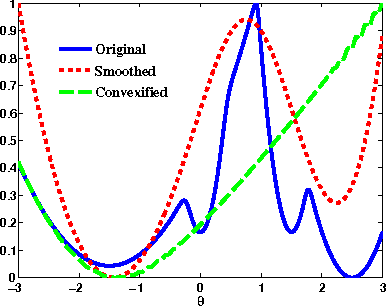
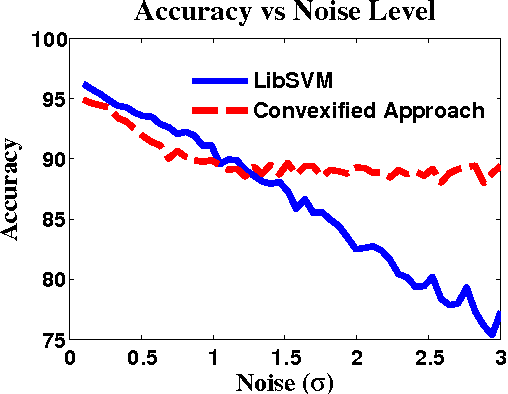
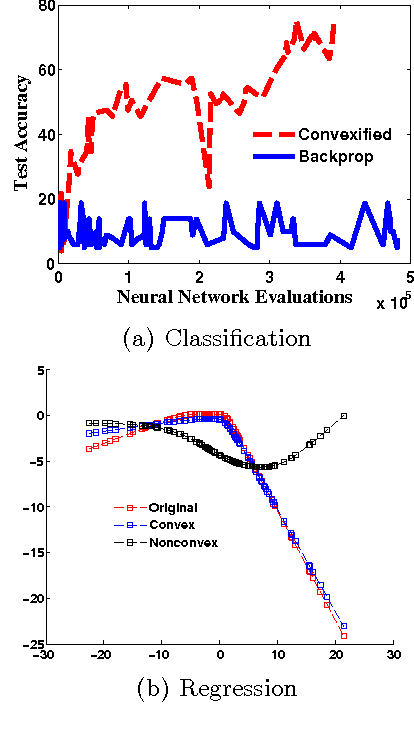
We develop a framework for convexifying a fairly general class of optimization problems. Under additional assumptions, we analyze the suboptimality of the solution to the convexified problem relative to the original nonconvex problem and prove additive approximation guarantees. We then develop algorithms based on stochastic gradient methods to solve the resulting optimization problems and show bounds on convergence rates. %We show a simple application of this framework to supervised learning, where one can perform integration explicitly and can use standard (non-stochastic) optimization algorithms with better convergence guarantees. We then extend this framework to apply to a general class of discrete-time dynamical systems. In this context, our convexification approach falls under the well-studied paradigm of risk-sensitive Markov Decision Processes. We derive the first known model-based and model-free policy gradient optimization algorithms with guaranteed convergence to the optimal solution. Finally, we present numerical results validating our formulation in different applications.