Graphical Newton
Paper and Code
Oct 08, 2017
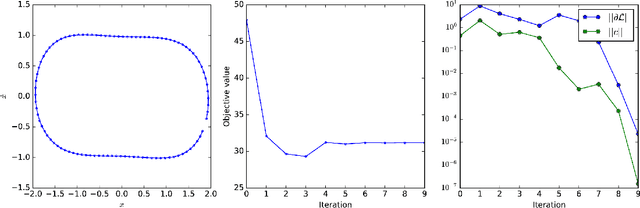
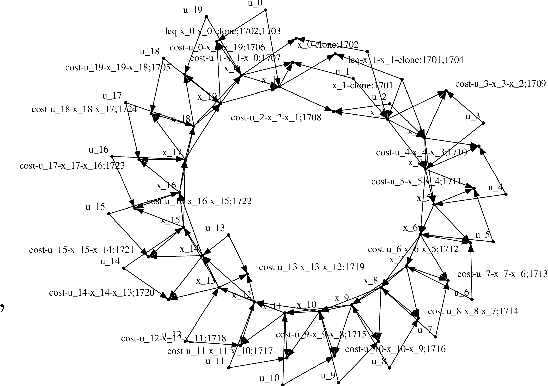
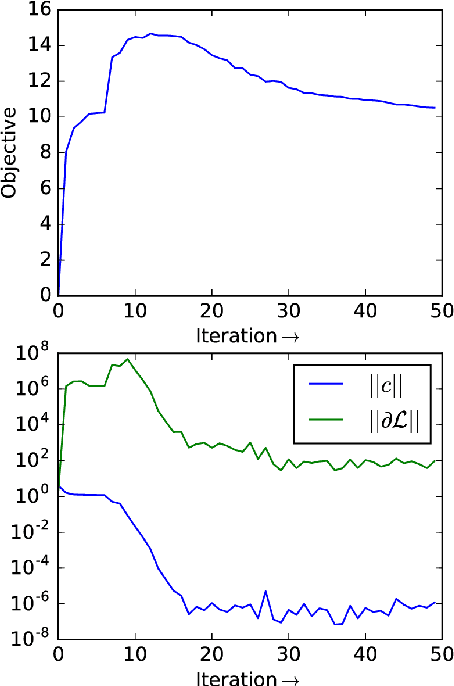
Computing the Newton step for a generic function $f: \mathbb{R}^N \rightarrow \mathbb{R}$ takes $O(N^{3})$ flops. In this paper, we explore avenues for reducing this bound, when the computational structure of $f$ is known beforehand. It is shown that the Newton step can be computed in time, linear in the size of the computational-graph, and cubic in its tree-width.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge