Universal Convexification via Risk-Aversion
Paper and Code
Jun 03, 2014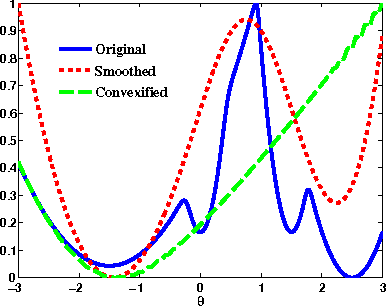
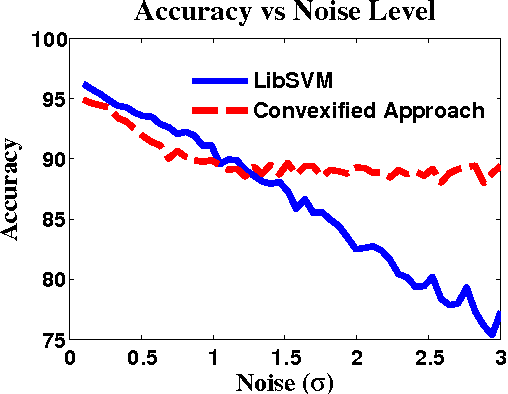
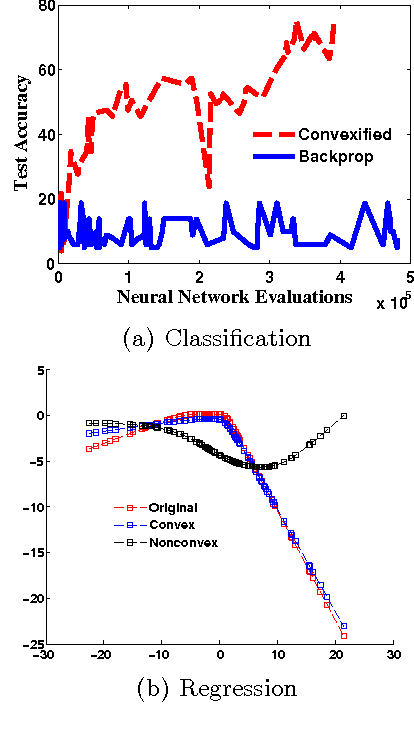
We develop a framework for convexifying a fairly general class of optimization problems. Under additional assumptions, we analyze the suboptimality of the solution to the convexified problem relative to the original nonconvex problem and prove additive approximation guarantees. We then develop algorithms based on stochastic gradient methods to solve the resulting optimization problems and show bounds on convergence rates. %We show a simple application of this framework to supervised learning, where one can perform integration explicitly and can use standard (non-stochastic) optimization algorithms with better convergence guarantees. We then extend this framework to apply to a general class of discrete-time dynamical systems. In this context, our convexification approach falls under the well-studied paradigm of risk-sensitive Markov Decision Processes. We derive the first known model-based and model-free policy gradient optimization algorithms with guaranteed convergence to the optimal solution. Finally, we present numerical results validating our formulation in different applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge