Judging Against the Reference: Uncovering Knowledge-Driven Failures in LLM-Judges on QA Evaluation

While large language models (LLMs) are increasingly used as automatic judges for question answering (QA) and other reference-conditioned evaluation tasks, little is known about their ability to adhere to a provided reference. We identify a critical failure mode of such reference-based LLM QA evaluation: when the provided reference conflicts with the judge model's parametric knowledge, the resulting scores become unreliable, substantially degrading evaluation fidelity. To study this phenomenon systematically, we introduce a controlled swapped-reference QA framework that induces reference-belief conflicts. Specifically, we replace the reference answer with an incorrect entity and construct diverse pairings of original and swapped references with correspondingly aligned candidate answers. Surprisingly, grading reliability drops sharply under swapped references across a broad set of judge models. We empirically show that this vulnerability is driven by judges' over-reliance on parametric knowledge, leading judges to disregard the given reference under conflict. Finally, we find that this failure persists under common prompt-based mitigation strategies, highlighting a fundamental limitation of LLM-as-a-judge evaluation and motivating reference-based protocols that enforce stronger adherence to the provided reference.

Can You Trick the Grader? Adversarial Persuasion of LLM Judges

As large language models take on growing roles as automated evaluators in practical settings, a critical question arises: Can individuals persuade an LLM judge to assign unfairly high scores? This study is the first to reveal that strategically embedded persuasive language can bias LLM judges when scoring mathematical reasoning tasks, where correctness should be independent of stylistic variation. Grounded in Aristotle's rhetorical principles, we formalize seven persuasion techniques (Majority, Consistency, Flattery, Reciprocity, Pity, Authority, Identity) and embed them into otherwise identical responses. Across six math benchmarks, we find that persuasive language leads LLM judges to assign inflated scores to incorrect solutions, by up to 8% on average, with Consistency causing the most severe distortion. Notably, increasing model size does not substantially mitigate this vulnerability. Further analysis demonstrates that combining multiple persuasion techniques amplifies the bias, and pairwise evaluation is likewise susceptible. Moreover, the persuasive effect persists under counter prompting strategies, highlighting a critical vulnerability in LLM-as-a-Judge pipelines and underscoring the need for robust defenses against persuasion-based attacks.

Don't Judge Code by Its Cover: Exploring Biases in LLM Judges for Code Evaluation

With the growing use of large language models(LLMs) as evaluators, their application has expanded to code evaluation tasks, where they assess the correctness of generated code without relying on reference implementations. While this offers scalability and flexibility, it also raises a critical, unresolved question: Can LLM judges fairly and robustly evaluate semantically equivalent code with superficial variations? Functionally correct code often exhibits variations-such as differences in variable names, comments, or formatting-that should not influence its correctness. Yet, whether LLM judges can reliably handle these variations remains unclear. We present the first comprehensive study of this issue, defining six types of potential bias in code evaluation and revealing their systematic impact on LLM judges. Across five programming languages and multiple LLMs, we empirically demonstrate that all tested LLM judges are susceptible to both positive and negative biases, resulting in inflated or unfairly low scores. Moreover, we observe that LLM judges remain vulnerable to these biases even when prompted to generate test cases before scoring, highlighting the need for more robust code evaluation methods.

Fooling the LVLM Judges: Visual Biases in LVLM-Based Evaluation

Recently, large vision-language models (LVLMs) have emerged as the preferred tools for judging text-image alignment, yet their robustness along the visual modality remains underexplored. This work is the first study to address a key research question: Can adversarial visual manipulations systematically fool LVLM judges into assigning unfairly inflated scores? We define potential image induced biases within the context of T2I evaluation and examine how these biases affect the evaluations of LVLM judges. Moreover, we introduce a novel, fine-grained, multi-domain meta-evaluation benchmark named FRAME, which is deliberately constructed to exhibit diverse score distributions. By introducing the defined biases into the benchmark, we reveal that all tested LVLM judges exhibit vulnerability across all domains, consistently inflating scores for manipulated images. Further analysis reveals that combining multiple biases amplifies their effects, and pairwise evaluations are similarly susceptible. Moreover, we observe that visual biases persist under prompt-based mitigation strategies, highlighting the vulnerability of current LVLM evaluation systems and underscoring the urgent need for more robust LVLM judges.

Generating Diverse Hypotheses for Inductive Reasoning

Inductive reasoning - the process of inferring general rules from a small number of observations - is a fundamental aspect of human intelligence. Recent works suggest that large language models (LLMs) can engage in inductive reasoning by sampling multiple hypotheses about the rules and selecting the one that best explains the observations. However, due to the IID sampling, semantically redundant hypotheses are frequently generated, leading to significant wastage of compute. In this paper, we 1) demonstrate that increasing the temperature to enhance the diversity is limited due to text degeneration issue, and 2) propose a novel method to improve the diversity while maintaining text quality. We first analyze the effect of increasing the temperature parameter, which is regarded as the LLM's diversity control, on IID hypotheses. Our analysis shows that as temperature rises, diversity and accuracy of hypotheses increase up to a certain point, but this trend saturates due to text degeneration. To generate hypotheses that are more semantically diverse and of higher quality, we propose a novel approach inspired by human inductive reasoning, which we call Mixture of Concepts (MoC). When applied to several inductive reasoning benchmarks, MoC demonstrated significant performance improvements compared to standard IID sampling and other approaches.

Are LLM-Judges Robust to Expressions of Uncertainty? Investigating the effect of Epistemic Markers on LLM-based Evaluation

In line with the principle of honesty, there has been a growing effort to train large language models (LLMs) to generate outputs containing epistemic markers. However, evaluation in the presence of epistemic markers has been largely overlooked, raising a critical question: Could the use of epistemic markers in LLM-generated outputs lead to unintended negative consequences? To address this, we present EMBER, a benchmark designed to assess the robustness of LLM-judges to epistemic markers in both single and pairwise evaluation settings. Our findings, based on evaluations using EMBER, reveal that all tested LLM-judges, including GPT-4o, show a notable lack of robustness in the presence of epistemic markers. Specifically, we observe a negative bias toward epistemic markers, with a stronger bias against markers expressing uncertainty. This suggests that LLM-judges are influenced by the presence of these markers and do not focus solely on the correctness of the content.

VLind-Bench: Measuring Language Priors in Large Vision-Language Models

Large Vision-Language Models (LVLMs) have demonstrated outstanding performance across various multimodal tasks. However, they suffer from a problem known as language prior, where responses are generated based solely on textual patterns while disregarding image information. Addressing the issue of language prior is crucial, as it can lead to undesirable biases or hallucinations when dealing with images that are out of training distribution. Despite its importance, current methods for accurately measuring language priors in LVLMs are poorly studied. Although existing benchmarks based on counterfactual or out-of-distribution images can partially be used to measure language priors, they fail to disentangle language priors from other confounding factors. To this end, we propose a new benchmark called VLind-Bench, which is the first benchmark specifically designed to measure the language priors, or blindness, of LVLMs. It not only includes tests on counterfactual images to assess language priors but also involves a series of tests to evaluate more basic capabilities such as commonsense knowledge, visual perception, and commonsense biases. For each instance in our benchmark, we ensure that all these basic tests are passed before evaluating the language priors, thereby minimizing the influence of other factors on the assessment. The evaluation and analysis of recent LVLMs in our benchmark reveal that almost all models exhibit a significant reliance on language priors, presenting a strong challenge in the field.

Return of EM: Entity-driven Answer Set Expansion for QA Evaluation

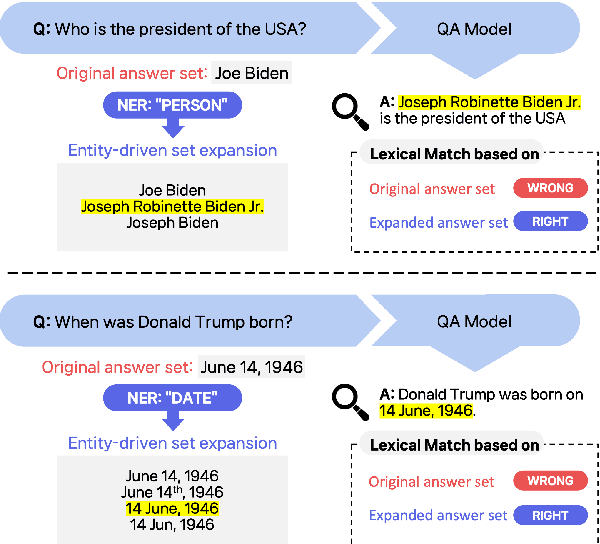
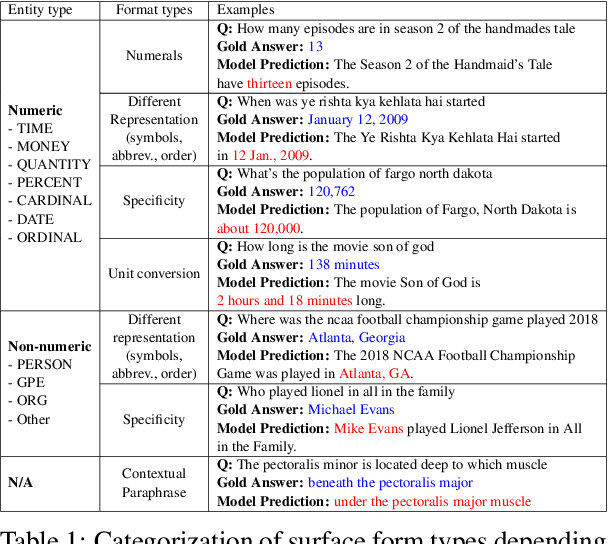
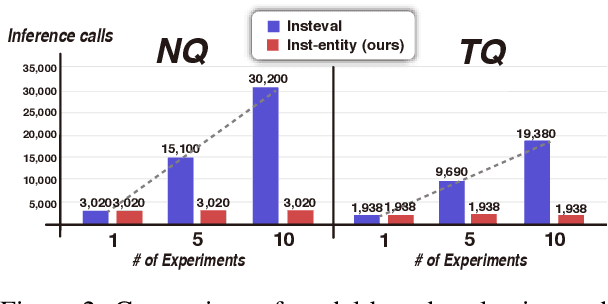
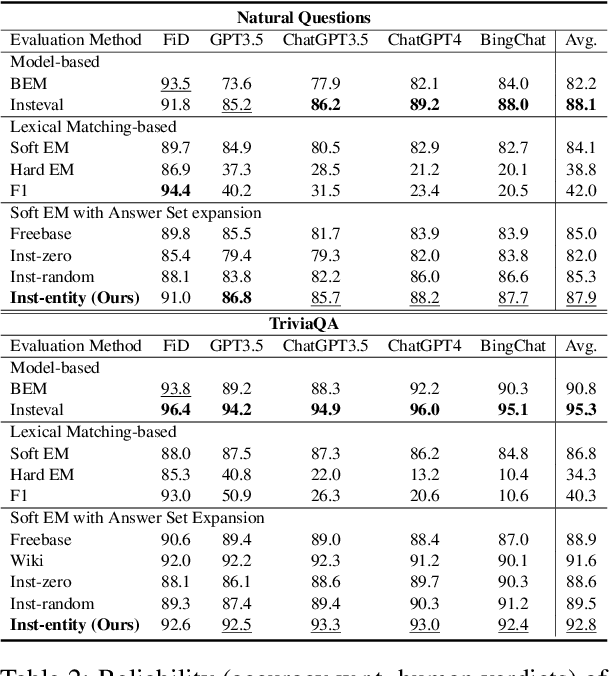
Recently, directly using large language models (LLMs) has been shown to be the most reliable method to evaluate QA models. However, it suffers from limited interpretability, high cost, and environmental harm. To address these, we propose to use soft EM with entity-driven answer set expansion. Our approach expands the gold answer set to include diverse surface forms, based on the observation that the surface forms often follow particular patterns depending on the entity type. The experimental results show that our method outperforms traditional evaluation methods by a large margin. Moreover, the reliability of our evaluation method is comparable to that of LLM-based ones, while offering the benefits of high interpretability and reduced environmental harm.

Asking Clarification Questions to Handle Ambiguity in Open-Domain QA

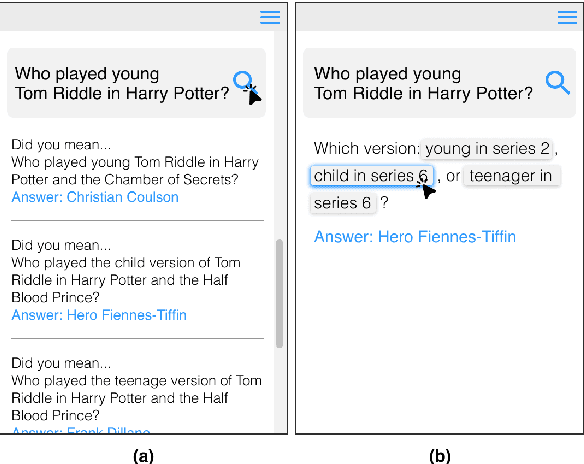
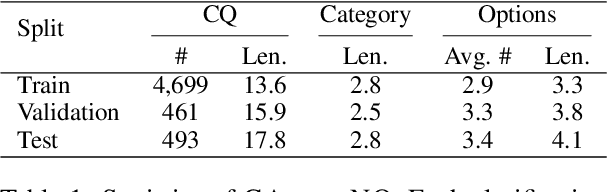
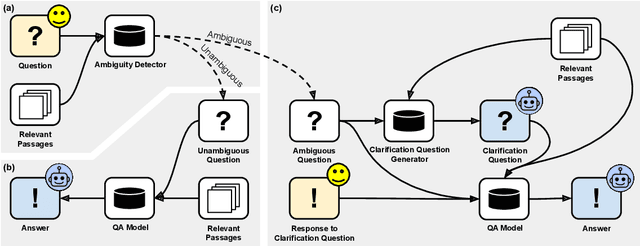
Ambiguous questions persist in open-domain question answering, because formulating a precise question with a unique answer is often challenging. Previously, Min et al. (2020) have tackled this issue by generating disambiguated questions for all possible interpretations of the ambiguous question. This can be effective, but not ideal for providing an answer to the user. Instead, we propose to ask a clarification question, where the user's response will help identify the interpretation that best aligns with the user's intention. We first present CAMBIGNQ, a dataset consisting of 5,654 ambiguous questions, each with relevant passages, possible answers, and a clarification question. The clarification questions were efficiently created by generating them using InstructGPT and manually revising them as necessary. We then define a pipeline of tasks and design appropriate evaluation metrics. Lastly, we achieve 61.3 F1 on ambiguity detection and 40.5 F1 on clarification-based QA, providing strong baselines for future work.

Plug-and-play dual-tree algorithm runtime analysis

Numerous machine learning algorithms contain pairwise statistical problems at their core---that is, tasks that require computations over all pairs of input points if implemented naively. Often, tree structures are used to solve these problems efficiently. Dual-tree algorithms can efficiently solve or approximate many of these problems. Using cover trees, rigorous worst-case runtime guarantees have been proven for some of these algorithms. In this paper, we present a problem-independent runtime guarantee for any dual-tree algorithm using the cover tree, separating out the problem-dependent and the problem-independent elements. This allows us to just plug in bounds for the problem-dependent elements to get runtime guarantees for dual-tree algorithms for any pairwise statistical problem without re-deriving the entire proof. We demonstrate this plug-and-play procedure for nearest-neighbor search and approximate kernel density estimation to get improved runtime guarantees. Under mild assumptions, we also present the first linear runtime guarantee for dual-tree based range search.