William B. March
ASKIT: Approximate Skeletonization Kernel-Independent Treecode in High Dimensions
Mar 13, 2015



Abstract:We present a fast algorithm for kernel summation problems in high-dimensions. These problems appear in computational physics, numerical approximation, non-parametric statistics, and machine learning. In our context, the sums depend on a kernel function that is a pair potential defined on a dataset of points in a high-dimensional Euclidean space. A direct evaluation of the sum scales quadratically with the number of points. Fast kernel summation methods can reduce this cost to linear complexity, but the constants involved do not scale well with the dimensionality of the dataset. The main algorithmic components of fast kernel summation algorithms are the separation of the kernel sum between near and far field (which is the basis for pruning) and the efficient and accurate approximation of the far field. We introduce novel methods for pruning and approximating the far field. Our far field approximation requires only kernel evaluations and does not use analytic expansions. Pruning is not done using bounding boxes but rather combinatorially using a sparsified nearest-neighbor graph of the input. The time complexity of our algorithm depends linearly on the ambient dimension. The error in the algorithm depends on the low-rank approximability of the far field, which in turn depends on the kernel function and on the intrinsic dimensionality of the distribution of the points. The error of the far field approximation does not depend on the ambient dimension. We present the new algorithm along with experimental results that demonstrate its performance. We report results for Gaussian kernel sums for 100 million points in 64 dimensions, for one million points in 1000 dimensions, and for problems in which the Gaussian kernel has a variable bandwidth. To the best of our knowledge, all of these experiments are impossible or prohibitively expensive with existing fast kernel summation methods.
Far-Field Compression for Fast Kernel Summation Methods in High Dimensions
Feb 13, 2015



Abstract:We consider fast kernel summations in high dimensions: given a large set of points in $d$ dimensions (with $d \gg 3$) and a pair-potential function (the {\em kernel} function), we compute a weighted sum of all pairwise kernel interactions for each point in the set. Direct summation is equivalent to a (dense) matrix-vector multiplication and scales quadratically with the number of points. Fast kernel summation algorithms reduce this cost to log-linear or linear complexity. Treecodes and Fast Multipole Methods (FMMs) deliver tremendous speedups by constructing approximate representations of interactions of points that are far from each other. In algebraic terms, these representations correspond to low-rank approximations of blocks of the overall interaction matrix. Existing approaches require an excessive number of kernel evaluations with increasing $d$ and number of points in the dataset. To address this issue, we use a randomized algebraic approach in which we first sample the rows of a block and then construct its approximate, low-rank interpolative decomposition. We examine the feasibility of this approach theoretically and experimentally. We provide a new theoretical result showing a tighter bound on the reconstruction error from uniformly sampling rows than the existing state-of-the-art. We demonstrate that our sampling approach is competitive with existing (but prohibitively expensive) methods from the literature. We also construct kernel matrices for the Laplacian, Gaussian, and polynomial kernels -- all commonly used in physics and data analysis. We explore the numerical properties of blocks of these matrices, and show that they are amenable to our approach. Depending on the data set, our randomized algorithm can successfully compute low rank approximations in high dimensions. We report results for data sets with ambient dimensions from four to 1,000.
Plug-and-play dual-tree algorithm runtime analysis
Jan 21, 2015


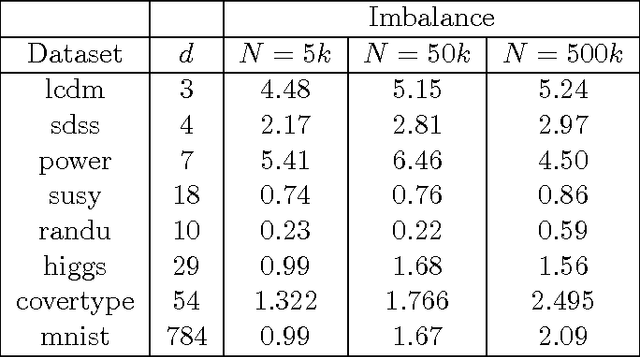
Abstract:Numerous machine learning algorithms contain pairwise statistical problems at their core---that is, tasks that require computations over all pairs of input points if implemented naively. Often, tree structures are used to solve these problems efficiently. Dual-tree algorithms can efficiently solve or approximate many of these problems. Using cover trees, rigorous worst-case runtime guarantees have been proven for some of these algorithms. In this paper, we present a problem-independent runtime guarantee for any dual-tree algorithm using the cover tree, separating out the problem-dependent and the problem-independent elements. This allows us to just plug in bounds for the problem-dependent elements to get runtime guarantees for dual-tree algorithms for any pairwise statistical problem without re-deriving the entire proof. We demonstrate this plug-and-play procedure for nearest-neighbor search and approximate kernel density estimation to get improved runtime guarantees. Under mild assumptions, we also present the first linear runtime guarantee for dual-tree based range search.
MLPACK: A Scalable C++ Machine Learning Library
Oct 23, 2012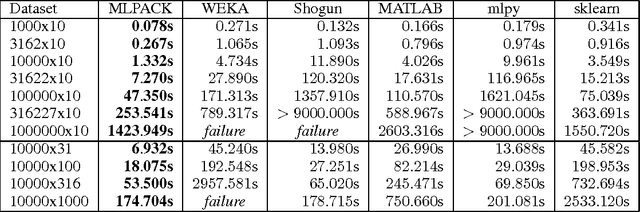
Abstract:MLPACK is a state-of-the-art, scalable, multi-platform C++ machine learning library released in late 2011 offering both a simple, consistent API accessible to novice users and high performance and flexibility to expert users by leveraging modern features of C++. MLPACK provides cutting-edge algorithms whose benchmarks exhibit far better performance than other leading machine learning libraries. MLPACK version 1.0.3, licensed under the LGPL, is available at http://www.mlpack.org.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge