NTIRE 2025 challenge on Text to Image Generation Model Quality Assessment

This paper reports on the NTIRE 2025 challenge on Text to Image (T2I) generation model quality assessment, which will be held in conjunction with the New Trends in Image Restoration and Enhancement Workshop (NTIRE) at CVPR 2025. The aim of this challenge is to address the fine-grained quality assessment of text-to-image generation models. This challenge evaluates text-to-image models from two aspects: image-text alignment and image structural distortion detection, and is divided into the alignment track and the structural track. The alignment track uses the EvalMuse-40K, which contains around 40K AI-Generated Images (AIGIs) generated by 20 popular generative models. The alignment track has a total of 371 registered participants. A total of 1,883 submissions are received in the development phase, and 507 submissions are received in the test phase. Finally, 12 participating teams submitted their models and fact sheets. The structure track uses the EvalMuse-Structure, which contains 10,000 AI-Generated Images (AIGIs) with corresponding structural distortion mask. A total of 211 participants have registered in the structure track. A total of 1155 submissions are received in the development phase, and 487 submissions are received in the test phase. Finally, 8 participating teams submitted their models and fact sheets. Almost all methods have achieved better results than baseline methods, and the winning methods in both tracks have demonstrated superior prediction performance on T2I model quality assessment.

MobileIQA: Exploiting Mobile-level Diverse Opinion Network For No-Reference Image Quality Assessment Using Knowledge Distillation

With the rising demand for high-resolution (HR) images, No-Reference Image Quality Assessment (NR-IQA) gains more attention, as it can ecaluate image quality in real-time on mobile devices and enhance user experience. However, existing NR-IQA methods often resize or crop the HR images into small resolution, which leads to a loss of important details. And most of them are of high computational complexity, which hinders their application on mobile devices due to limited computational resources. To address these challenges, we propose MobileIQA, a novel approach that utilizes lightweight backbones to efficiently assess image quality while preserving image details through high-resolution input. MobileIQA employs the proposed multi-view attention learning (MAL) module to capture diverse opinions, simulating subjective opinions provided by different annotators during the dataset annotation process. The model uses a teacher model to guide the learning of a student model through knowledge distillation. This method significantly reduces computational complexity while maintaining high performance. Experiments demonstrate that MobileIQA outperforms novel IQA methods on evaluation metrics and computational efficiency. The code is available at https://github.com/chencn2020/MobileIQA.

EP-GIG Priors and Applications in Bayesian Sparse Learning

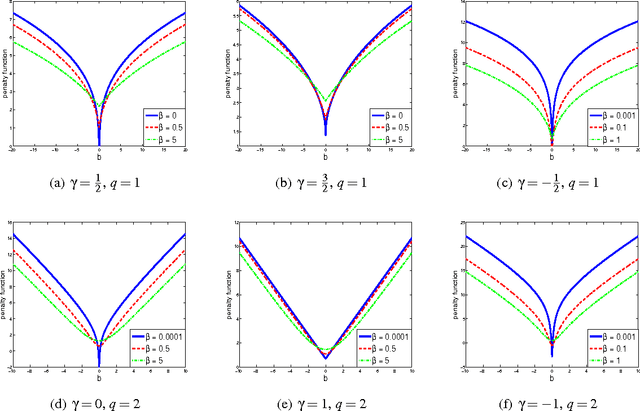
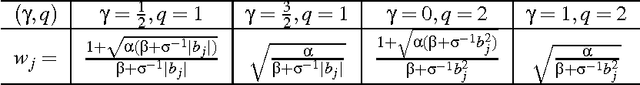
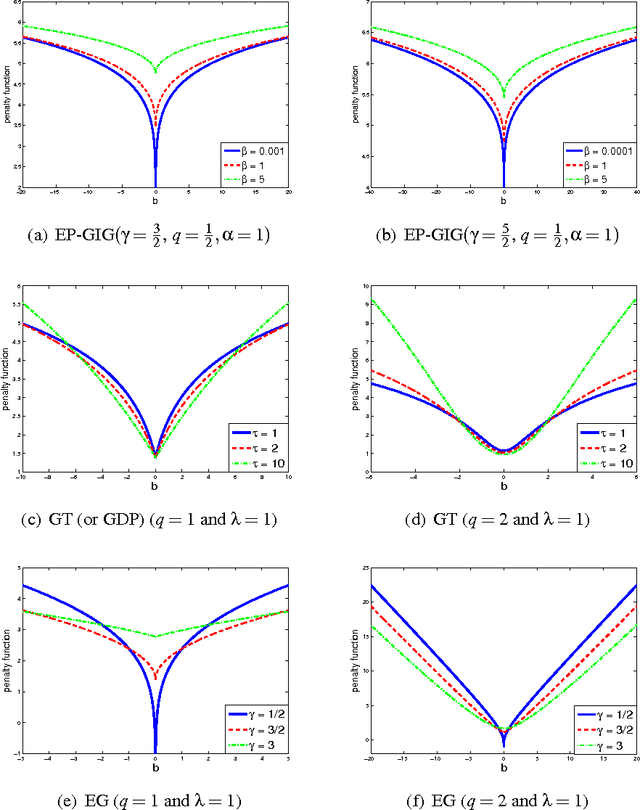
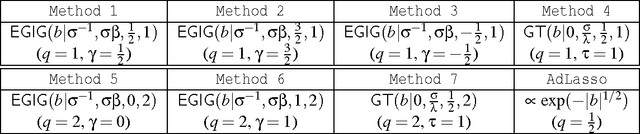
In this paper we propose a novel framework for the construction of sparsity-inducing priors. In particular, we define such priors as a mixture of exponential power distributions with a generalized inverse Gaussian density (EP-GIG). EP-GIG is a variant of generalized hyperbolic distributions, and the special cases include Gaussian scale mixtures and Laplace scale mixtures. Furthermore, Laplace scale mixtures can subserve a Bayesian framework for sparse learning with nonconvex penalization. The densities of EP-GIG can be explicitly expressed. Moreover, the corresponding posterior distribution also follows a generalized inverse Gaussian distribution. These properties lead us to EM algorithms for Bayesian sparse learning. We show that these algorithms bear an interesting resemblance to iteratively re-weighted $\ell_2$ or $\ell_1$ methods. In addition, we present two extensions for grouped variable selection and logistic regression.