Real-time Motion Segmentation with Event-based Normal Flow

Event-based cameras are bio-inspired sensors with pixels that independently and asynchronously respond to brightness changes at microsecond resolution, offering the potential to handle visual tasks in challenging scenarios. However, due to the sparse information content in individual events, directly processing the raw event data to solve vision tasks is highly inefficient, which severely limits the applicability of state-of-the-art methods in real-time tasks, such as motion segmentation, a fundamental task for dynamic scene understanding. Incorporating normal flow as an intermediate representation to compress motion information from event clusters within a localized region provides a more effective solution. In this work, we propose a normal flow-based motion segmentation framework for event-based vision. Leveraging the dense normal flow directly learned from event neighborhoods as input, we formulate the motion segmentation task as an energy minimization problem solved via graph cuts, and optimize it iteratively with normal flow clustering and motion model fitting. By using a normal flow-based motion model initialization and fitting method, the proposed system is able to efficiently estimate the motion models of independently moving objects with only a limited number of candidate models, which significantly reduces the computational complexity and ensures real-time performance, achieving nearly a 800x speedup in comparison to the open-source state-of-the-art method. Extensive evaluations on multiple public datasets fully demonstrate the accuracy and efficiency of our framework.

PersonaLedger: Generating Realistic Financial Transactions with Persona Conditioned LLMs and Rule Grounded Feedback

Strict privacy regulations limit access to real transaction data, slowing open research in financial AI. Synthetic data can bridge this gap, but existing generators do not jointly achieve behavioral diversity and logical groundedness. Rule-driven simulators rely on hand-crafted workflows and shallow stochasticity, which miss the richness of human behavior. Learning-based generators such as GANs capture correlations yet often violate hard financial constraints and still require training on private data. We introduce PersonaLedger, a generation engine that uses a large language model conditioned on rich user personas to produce diverse transaction streams, coupled with an expert configurable programmatic engine that maintains correctness. The LLM and engine interact in a closed loop: after each event, the engine updates the user state, enforces financial rules, and returns a context aware "nextprompt" that guides the LLM toward feasible next actions. With this engine, we create a public dataset of 30 million transactions from 23,000 users and a benchmark suite with two tasks, illiquidity classification and identity theft segmentation. PersonaLedger offers a realistic, privacy preserving resource that supports rigorous evaluation of forecasting and anomaly detection models. PersonaLedger offers the community a rich, realistic, and privacy preserving resource -- complete with code, rules, and generation logs -- to accelerate innovation in financial AI and enable rigorous, reproducible evaluation.

A Real-Time Event-Based Normal Flow Estimator

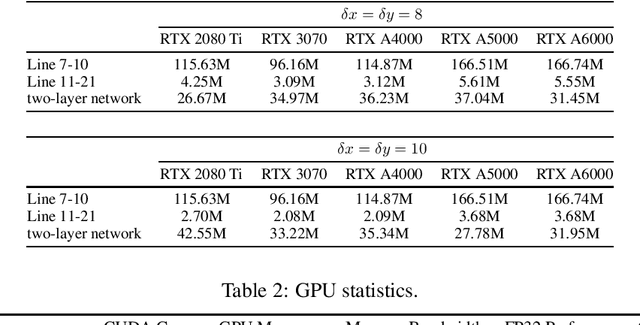
This paper presents a real-time, asynchronous, event-based normal flow estimator. It follows the same algorithm as Learning Normal Flow Directly From Event Neighborhoods, but with a more optimized implementation. The original method treats event slices as 3D point clouds, encodes each event's local geometry into a fixed-length vector, and uses a multi-layer perceptron to predict normal flow. It constructs representations by multiplying an adjacency matrix with a feature matrix, resulting in quadratic time complexity with respect to the number of events. In contrast, we leverage the fact that event coordinates are integers and reformulate the representation step as a pooling operation. This achieves the same effect as the adjacency matrix but with much lower computational cost. As a result, our method supports real-time normal flow prediction on event cameras. Our estimator uses 1 GB of CUDA memory and runs at 4 million normal flows per second on an RTX 3070, or 6 million per second on an RTX A5000. We release the CUDA implementation along with a Python interface at https://github.com/dhyuan99/VecKM_flow_cpp.

Learning Normal Flow Directly From Event Neighborhoods

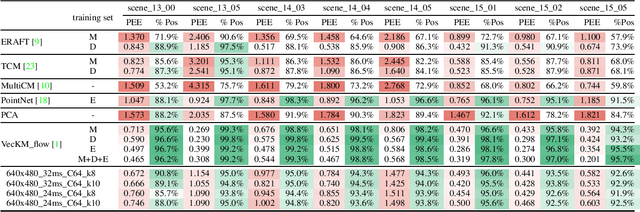
Event-based motion field estimation is an important task. However, current optical flow methods face challenges: learning-based approaches, often frame-based and relying on CNNs, lack cross-domain transferability, while model-based methods, though more robust, are less accurate. To address the limitations of optical flow estimation, recent works have focused on normal flow, which can be more reliably measured in regions with limited texture or strong edges. However, existing normal flow estimators are predominantly model-based and suffer from high errors. In this paper, we propose a novel supervised point-based method for normal flow estimation that overcomes the limitations of existing event learning-based approaches. Using a local point cloud encoder, our method directly estimates per-event normal flow from raw events, offering multiple unique advantages: 1) It produces temporally and spatially sharp predictions. 2) It supports more diverse data augmentation, such as random rotation, to improve robustness across various domains. 3) It naturally supports uncertainty quantification via ensemble inference, which benefits downstream tasks. 4) It enables training and inference on undistorted data in normalized camera coordinates, improving transferability across cameras. Extensive experiments demonstrate our method achieves better and more consistent performance than state-of-the-art methods when transferred across different datasets. Leveraging this transferability, we train our model on the union of datasets and release it for public use. Finally, we introduce an egomotion solver based on a maximum-margin problem that uses normal flow and IMU to achieve strong performance in challenging scenarios.

Repurposing Pre-trained Video Diffusion Models for Event-based Video Interpolation

Video Frame Interpolation aims to recover realistic missing frames between observed frames, generating a high-frame-rate video from a low-frame-rate video. However, without additional guidance, the large motion between frames makes this problem ill-posed. Event-based Video Frame Interpolation (EVFI) addresses this challenge by using sparse, high-temporal-resolution event measurements as motion guidance. This guidance allows EVFI methods to significantly outperform frame-only methods. However, to date, EVFI methods have relied on a limited set of paired event-frame training data, severely limiting their performance and generalization capabilities. In this work, we overcome the limited data challenge by adapting pre-trained video diffusion models trained on internet-scale datasets to EVFI. We experimentally validate our approach on real-world EVFI datasets, including a new one that we introduce. Our method outperforms existing methods and generalizes across cameras far better than existing approaches.

A Linear Time and Space Local Point Cloud Geometry Encoder via Vectorized Kernel Mixture

We propose VecKM, a novel local point cloud geometry encoder that is descriptive, efficient and robust to noise. VecKM leverages a unique approach by vectorizing a kernel mixture to represent the local point clouds. Such representation is descriptive and robust to noise, which is supported by two theorems that confirm its ability to reconstruct and preserve the similarity of the local shape. Moreover, VecKM is the first successful attempt to reduce the computation and memory costs from $O(n^2+nKd)$ to $O(nd)$ by sacrificing a marginal constant factor, where $n$ is the size of the point cloud and $K$ is neighborhood size. The efficiency is primarily due to VecKM's unique factorizable property that eliminates the need of explicitly grouping points into neighborhoods. In the normal estimation task, VecKM demonstrates not only 100x faster inference speed but also strongest descriptiveness and robustness compared with existing popular encoders. In classification and segmentation tasks, integrating VecKM as a preprocessing module achieves consistently better performance than the PointNet, PointNet++, and point transformer baselines, and runs consistently faster by up to 10x.

Decodable and Sample Invariant Continuous Object Encoder

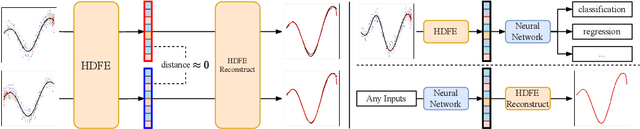
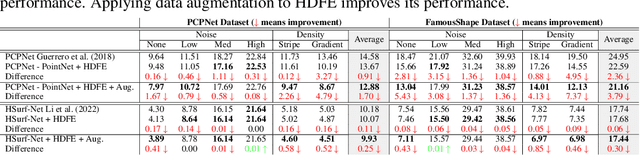
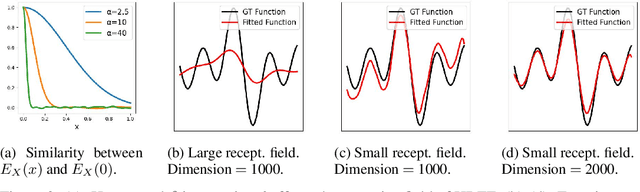
We propose Hyper-Dimensional Function Encoding (HDFE). Given samples of a continuous object (e.g. a function), HDFE produces an explicit vector representation of the given object, invariant to the sample distribution and density. Sample distribution and density invariance enables HDFE to consistently encode continuous objects regardless of their sampling, and therefore allows neural networks to receive continuous objects as inputs for machine learning tasks, such as classification and regression. Besides, HDFE does not require any training and is proved to map the object into an organized embedding space, which facilitates the training of the downstream tasks. In addition, the encoding is decodable, which enables neural networks to regress continuous objects by regressing their encodings. Therefore, HDFE serves as an interface for processing continuous objects. We apply HDFE to function-to-function mapping, where vanilla HDFE achieves competitive performance as the state-of-the-art algorithm. We apply HDFE to point cloud surface normal estimation, where a simple replacement from PointNet to HDFE leads to immediate 12% and 15% error reductions in two benchmarks. In addition, by integrating HDFE into the PointNet-based SOTA network, we improve the SOTA baseline by 2.5% and 1.7% in the same benchmarks.

Gluing Neural Networks Symbolically Through Hyperdimensional Computing

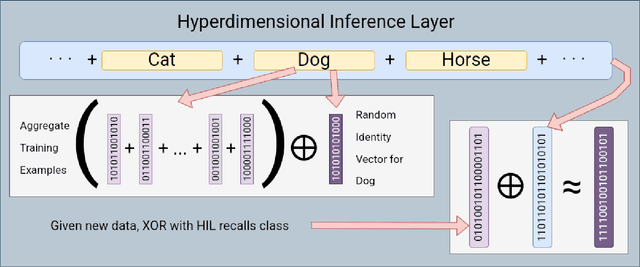
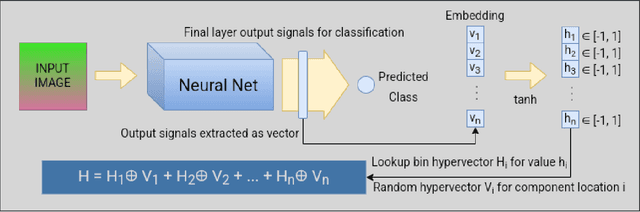
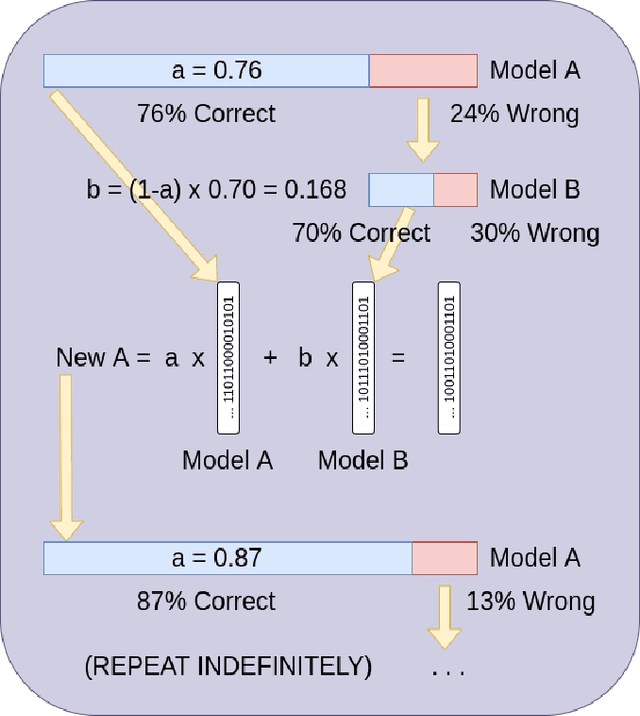
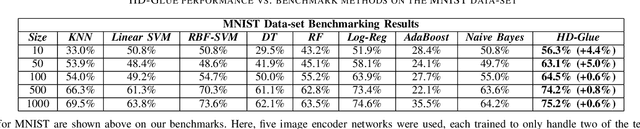
Hyperdimensional Computing affords simple, yet powerful operations to create long Hyperdimensional Vectors (hypervectors) that can efficiently encode information, be used for learning, and are dynamic enough to be modified on the fly. In this paper, we explore the notion of using binary hypervectors to directly encode the final, classifying output signals of neural networks in order to fuse differing networks together at the symbolic level. This allows multiple neural networks to work together to solve a problem, with little additional overhead. Output signals just before classification are encoded as hypervectors and bundled together through consensus summation to train a classification hypervector. This process can be performed iteratively and even on single neural networks by instead making a consensus of multiple classification hypervectors. We find that this outperforms the state of the art, or is on a par with it, while using very little overhead, as hypervector operations are extremely fast and efficient in comparison to the neural networks. This consensus process can learn online and even grow or lose models in real time. Hypervectors act as memories that can be stored, and even further bundled together over time, affording life long learning capabilities. Additionally, this consensus structure inherits the benefits of Hyperdimensional Computing, without sacrificing the performance of modern Machine Learning. This technique can be extrapolated to virtually any neural model, and requires little modification to employ - one simply requires recording the output signals of networks when presented with a testing example.