Gluing Neural Networks Symbolically Through Hyperdimensional Computing

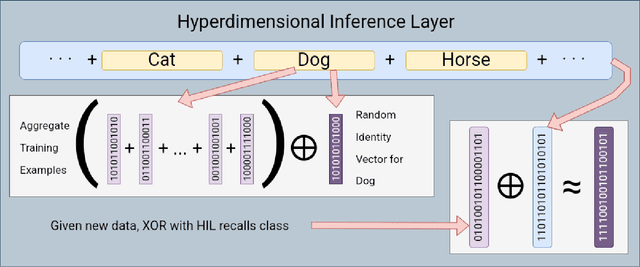
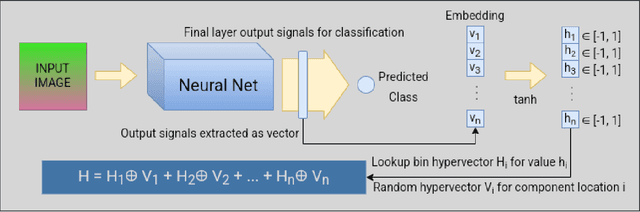
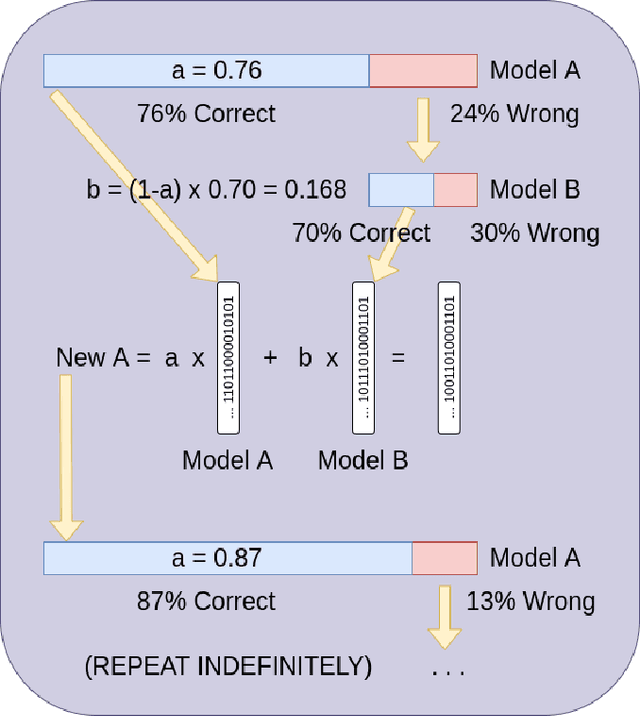
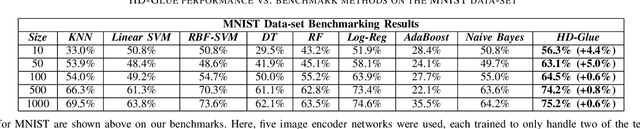
Hyperdimensional Computing affords simple, yet powerful operations to create long Hyperdimensional Vectors (hypervectors) that can efficiently encode information, be used for learning, and are dynamic enough to be modified on the fly. In this paper, we explore the notion of using binary hypervectors to directly encode the final, classifying output signals of neural networks in order to fuse differing networks together at the symbolic level. This allows multiple neural networks to work together to solve a problem, with little additional overhead. Output signals just before classification are encoded as hypervectors and bundled together through consensus summation to train a classification hypervector. This process can be performed iteratively and even on single neural networks by instead making a consensus of multiple classification hypervectors. We find that this outperforms the state of the art, or is on a par with it, while using very little overhead, as hypervector operations are extremely fast and efficient in comparison to the neural networks. This consensus process can learn online and even grow or lose models in real time. Hypervectors act as memories that can be stored, and even further bundled together over time, affording life long learning capabilities. Additionally, this consensus structure inherits the benefits of Hyperdimensional Computing, without sacrificing the performance of modern Machine Learning. This technique can be extrapolated to virtually any neural model, and requires little modification to employ - one simply requires recording the output signals of networks when presented with a testing example.

Representing Sets as Summed Semantic Vectors

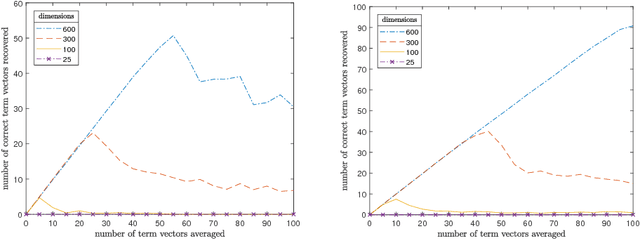
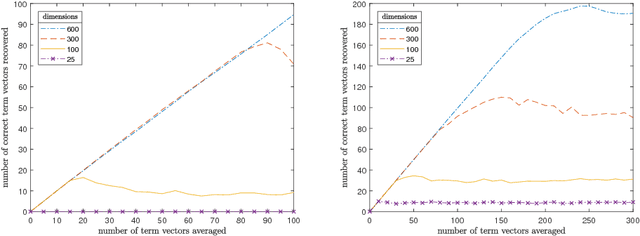
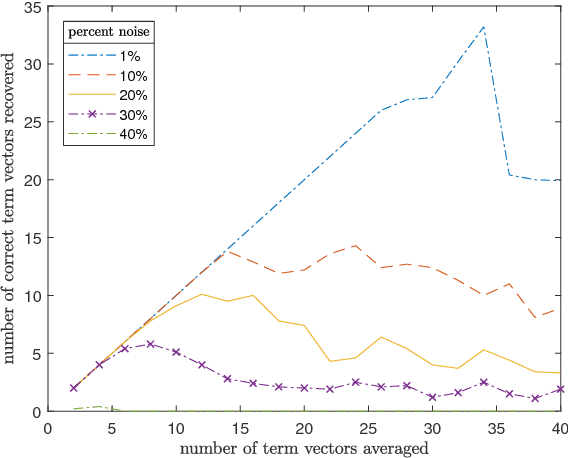
Representing meaning in the form of high dimensional vectors is a common and powerful tool in biologically inspired architectures. While the meaning of a set of concepts can be summarized by taking a (possibly weighted) sum of their associated vectors, this has generally been treated as a one-way operation. In this paper we show how a technique built to aid sparse vector decomposition allows in many cases the exact recovery of the inputs and weights to such a sum, allowing a single vector to represent an entire set of vectors from a dictionary. We characterize the number of vectors that can be recovered under various conditions, and explore several ways such a tool can be used for vector-based reasoning.