An Experimental Study of Data Heterogeneity in Federated Learning Methods for Medical Imaging

Federated learning enables multiple institutions to collaboratively train machine learning models on their local data in a privacy-preserving way. However, its distributed nature often leads to significant heterogeneity in data distributions across institutions. In this paper, we investigate the deleterious impact of a taxonomy of data heterogeneity regimes on federated learning methods, including quantity skew, label distribution skew, and imaging acquisition skew. We show that the performance degrades with the increasing degrees of data heterogeneity. We present several mitigation strategies to overcome performance drops from data heterogeneity, including weighted average for data quantity skew, weighted loss and batch normalization averaging for label distribution skew. The proposed optimizations to federated learning methods improve their capability of handling heterogeneity across institutions, which provides valuable guidance for the deployment of federated learning in real clinical applications.

The unreasonable effectiveness of Batch-Norm statistics in addressing catastrophic forgetting across medical institutions

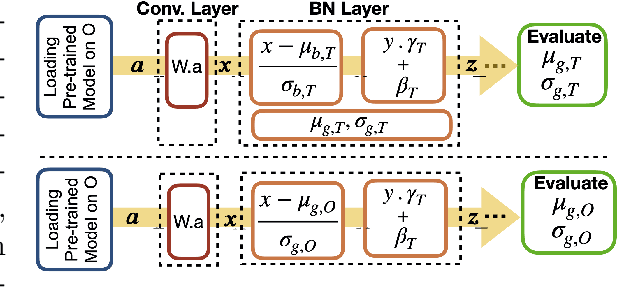
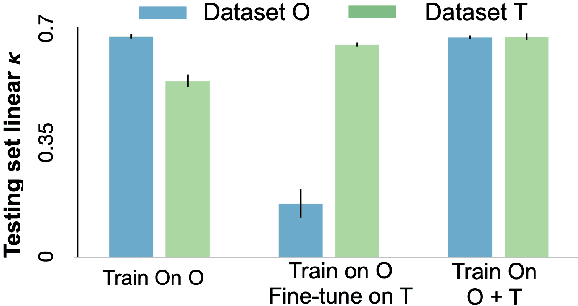
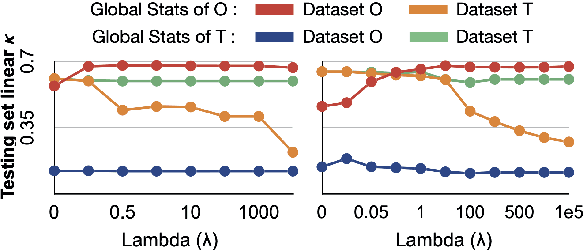
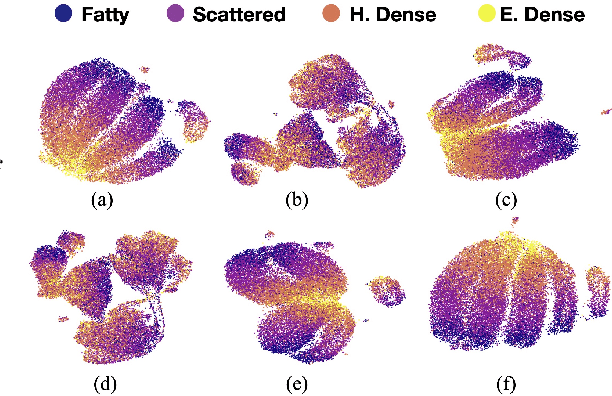
Model brittleness is a primary concern when deploying deep learning models in medical settings owing to inter-institution variations, like patient demographics and intra-institution variation, such as multiple scanner types. While simply training on the combined datasets is fraught with data privacy limitations, fine-tuning the model on subsequent institutions after training it on the original institution results in a decrease in performance on the original dataset, a phenomenon called catastrophic forgetting. In this paper, we investigate trade-off between model refinement and retention of previously learned knowledge and subsequently address catastrophic forgetting for the assessment of mammographic breast density. More specifically, we propose a simple yet effective approach, adapting Elastic weight consolidation (EWC) using the global batch normalization (BN) statistics of the original dataset. The results of this study provide guidance for the deployment of clinical deep learning models where continuous learning is needed for domain expansion.

Institutionally Distributed Deep Learning Networks

Deep learning has become a promising approach for automated medical diagnoses. When medical data samples are limited, collaboration among multiple institutions is necessary to achieve high algorithm performance. However, sharing patient data often has limitations due to technical, legal, or ethical concerns. In such cases, sharing a deep learning model is a more attractive alternative. The best method of performing such a task is unclear, however. In this study, we simulate the dissemination of learning deep learning network models across four institutions using various heuristics and compare the results with a deep learning model trained on centrally hosted patient data. The heuristics investigated include ensembling single institution models, single weight transfer, and cyclical weight transfer. We evaluated these approaches for image classification in three independent image collections (retinal fundus photos, mammography, and ImageNet). We find that cyclical weight transfer resulted in a performance (testing accuracy = 77.3%) that was closest to that of centrally hosted patient data (testing accuracy = 78.7%). We also found that there is an improvement in the performance of cyclical weight transfer heuristic with high frequency of weight transfer.

Piecewise convexity of artificial neural networks

Although artificial neural networks have shown great promise in applications including computer vision and speech recognition, there remains considerable practical and theoretical difficulty in optimizing their parameters. The seemingly unreasonable success of gradient descent methods in minimizing these non-convex functions remains poorly understood. In this work we offer some theoretical guarantees for networks with piecewise affine activation functions, which have in recent years become the norm. We prove three main results. Firstly, that the network is piecewise convex as a function of the input data. Secondly, that the network, considered as a function of the parameters in a single layer, all others held constant, is again piecewise convex. Finally, that the network as a function of all its parameters is piecewise multi-convex, a generalization of biconvexity. From here we characterize the local minima and stationary points of the training objective, showing that they minimize certain subsets of the parameter space. We then analyze the performance of two optimization algorithms on multi-convex problems: gradient descent, and a method which repeatedly solves a number of convex sub-problems. We prove necessary convergence conditions for the first algorithm and both necessary and sufficient conditions for the second, after introducing regularization to the objective. Finally, we remark on the remaining difficulty of the global optimization problem. Under the squared error objective, we show that by varying the training data, a single rectifier neuron admits local minima arbitrarily far apart, both in objective value and parameter space.