COVID-19 Lung Lesion Segmentation Using a Sparsely Supervised Mask R-CNN on Chest X-rays Automatically Computed from Volumetric CTs

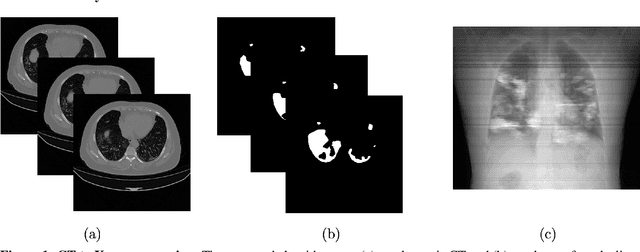
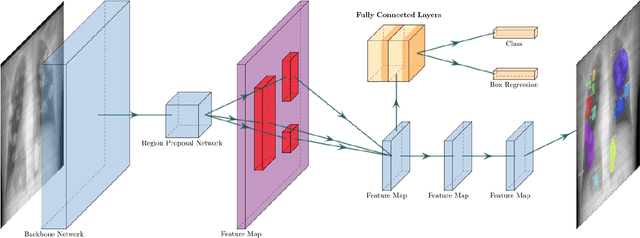
Chest X-rays of coronavirus disease 2019 (COVID-19) patients are frequently obtained to determine the extent of lung disease and are a valuable source of data for creating artificial intelligence models. Most work to date assessing disease severity on chest imaging has focused on segmenting computed tomography (CT) images; however, given that CTs are performed much less frequently than chest X-rays for COVID-19 patients, automated lung lesion segmentation on chest X-rays could be clinically valuable. There currently exists a universal shortage of chest X-rays with ground truth COVID-19 lung lesion annotations, and manually contouring lung opacities is a tedious, labor-intensive task. To accelerate severity detection and augment the amount of publicly available chest X-ray training data for supervised deep learning (DL) models, we leverage existing annotated CT images to generate frontal projection "chest X-ray" images for training COVID-19 chest X-ray models. In this paper, we propose an automated pipeline for segmentation of COVID-19 lung lesions on chest X-rays comprised of a Mask R-CNN trained on a mixed dataset of open-source chest X-rays and coronal X-ray projections computed from annotated volumetric CTs. On a test set containing 40 chest X-rays of COVID-19 positive patients, our model achieved IoU scores of 0.81 $\pm$ 0.03 and 0.79 $\pm$ 0.03 when trained on a dataset of 60 chest X-rays and on a mixed dataset of 10 chest X-rays and 50 projections from CTs, respectively. Our model far outperforms current baselines with limited supervised training and may assist in automated COVID-19 severity quantification on chest X-rays.

Probabilistic bounds on data sensitivity in deep rectifier networks

Neuron death is a complex phenomenon with implications for model trainability, but until recently it was measured only empirically. Recent articles have claimed that, as the depth of a rectifier neural network grows to infinity, the probability of finding a valid initialization decreases to zero. In this work, we provide a simple and rigorous proof of that result. Then, we show what happens when the width of each layer grows simultaneously with the depth. We derive both upper and lower bounds on the probability that a ReLU network is initialized to a trainable point, as a function of model hyperparameters. Contrary to previous claims, we show that it is possible to increase the depth of a network indefinitely, so long as the width increases as well. Furthermore, our bounds are asymptotically tight under reasonable assumptions: first, the upper bound coincides with the true probability for a single-layer network with the largest possible input set. Second, the true probability converges to our lower bound when the network width and depth both grow without limit. Our proof is based on the striking observation that very deep rectifier networks concentrate all outputs towards a single eigenvalue, in the sense that their normalized output variance goes to zero regardless of the network width. Finally, we develop a practical sign flipping scheme which guarantees with probability one that for a $k$-layer network, the ratio of living training data points is at least $2^{-k}$. We confirm our results with numerical simulations, suggesting that the actual improvement far exceeds the theoretical minimum. We also discuss how neuron death provides a theoretical interpretation for various network design choices such as batch normalization, residual layers and skip connections, and could inform the design of very deep neural networks.

CT organ segmentation using GPU data augmentation, unsupervised labels and IOU loss

Fully-convolutional neural networks have achieved superior performance in a variety of image segmentation tasks. However, their training requires laborious manual annotation of large datasets, as well as acceleration by parallel processors with high-bandwidth memory, such as GPUs. We show that simple models can achieve competitive accuracy for organ segmentation on CT images when trained with extensive data augmentation, which leverages existing graphics hardware to quickly apply geometric and photometric transformations to 3D image data. On 3 mm^3 CT volumes, our GPU implementation is 2.6-8X faster than a widely-used CPU version, including communication overhead. We also show how to automatically generate training labels using rudimentary morphological operations, which are efficiently computed by 3D Fourier transforms. We combined fully-automatic labels for the lungs and bone with semi-automatic ones for the liver, kidneys and bladder, to create a dataset of 130 labeled CT scans. To achieve the best results from data augmentation, our model uses the intersection-over-union (IOU) loss function, a close relative of the Dice loss. We discuss its mathematical properties and explain why it outperforms the usual weighted cross-entropy loss for unbalanced segmentation tasks. We conclude that there is no unique IOU loss function, as the naive one belongs to a broad family of functions with the same essential properties. When combining data augmentation with the IOU loss, our model achieves a Dice score of 78-92% for each organ. The trained model, code and dataset will be made publicly available, to further medical imaging research.

Piecewise convexity of artificial neural networks

Although artificial neural networks have shown great promise in applications including computer vision and speech recognition, there remains considerable practical and theoretical difficulty in optimizing their parameters. The seemingly unreasonable success of gradient descent methods in minimizing these non-convex functions remains poorly understood. In this work we offer some theoretical guarantees for networks with piecewise affine activation functions, which have in recent years become the norm. We prove three main results. Firstly, that the network is piecewise convex as a function of the input data. Secondly, that the network, considered as a function of the parameters in a single layer, all others held constant, is again piecewise convex. Finally, that the network as a function of all its parameters is piecewise multi-convex, a generalization of biconvexity. From here we characterize the local minima and stationary points of the training objective, showing that they minimize certain subsets of the parameter space. We then analyze the performance of two optimization algorithms on multi-convex problems: gradient descent, and a method which repeatedly solves a number of convex sub-problems. We prove necessary convergence conditions for the first algorithm and both necessary and sufficient conditions for the second, after introducing regularization to the objective. Finally, we remark on the remaining difficulty of the global optimization problem. Under the squared error objective, we show that by varying the training data, a single rectifier neuron admits local minima arbitrarily far apart, both in objective value and parameter space.