Is Model Collapse Inevitable? Breaking the Curse of Recursion by Accumulating Real and Synthetic Data

The proliferation of generative models, combined with pretraining on web-scale data, raises a timely question: what happens when these models are trained on their own generated outputs? Recent investigations into model-data feedback loops discovered that such loops can lead to model collapse, a phenomenon where performance progressively degrades with each model-fitting iteration until the latest model becomes useless. However, several recent papers studying model collapse assumed that new data replace old data over time rather than assuming data accumulate over time. In this paper, we compare these two settings and show that accumulating data prevents model collapse. We begin by studying an analytically tractable setup in which a sequence of linear models are fit to the previous models' predictions. Previous work showed if data are replaced, the test error increases linearly with the number of model-fitting iterations; we extend this result by proving that if data instead accumulate, the test error has a finite upper bound independent of the number of iterations. We next empirically test whether accumulating data similarly prevents model collapse by pretraining sequences of language models on text corpora. We confirm that replacing data does indeed cause model collapse, then demonstrate that accumulating data prevents model collapse; these results hold across a range of model sizes, architectures and hyperparameters. We further show that similar results hold for other deep generative models on real data: diffusion models for molecule generation and variational autoencoders for image generation. Our work provides consistent theoretical and empirical evidence that data accumulation mitigates model collapse.

The Unreasonable Ineffectiveness of the Deeper Layers

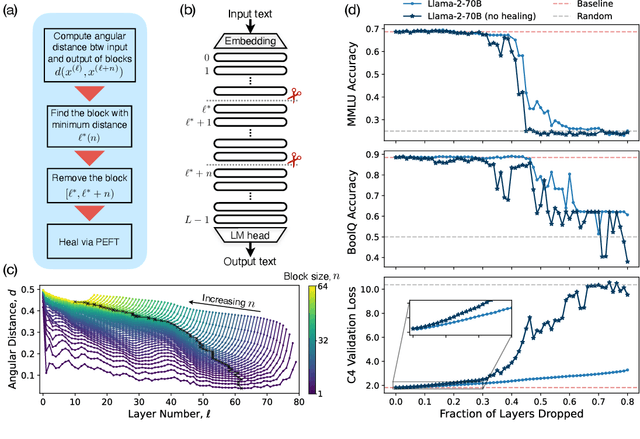
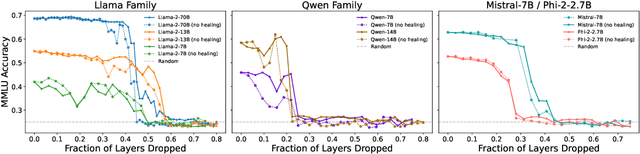
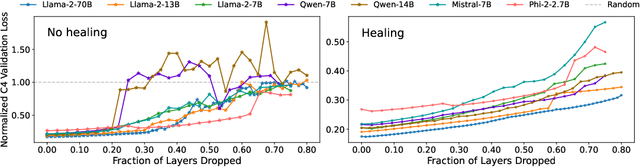
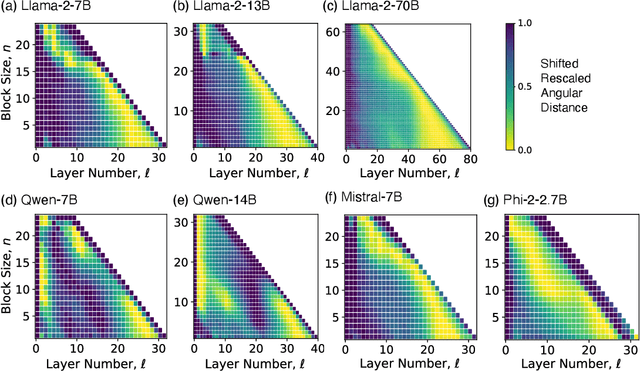
We empirically study a simple layer-pruning strategy for popular families of open-weight pretrained LLMs, finding minimal degradation of performance on different question-answering benchmarks until after a large fraction (up to half) of the layers are removed. To prune these models, we identify the optimal block of layers to prune by considering similarity across layers; then, to "heal" the damage, we perform a small amount of finetuning. In particular, we use parameter-efficient finetuning (PEFT) methods, specifically quantization and Low Rank Adapters (QLoRA), such that each of our experiments can be performed on a single A100 GPU. From a practical perspective, these results suggest that layer pruning methods can complement other PEFT strategies to further reduce computational resources of finetuning on the one hand, and can improve the memory and latency of inference on the other hand. From a scientific perspective, the robustness of these LLMs to the deletion of layers implies either that current pretraining methods are not properly leveraging the parameters in the deeper layers of the network or that the shallow layers play a critical role in storing knowledge.

Feature Learning and Generalization in Deep Networks with Orthogonal Weights

Fully-connected deep neural networks with weights initialized from independent Gaussian distributions can be tuned to criticality, which prevents the exponential growth or decay of signals propagating through the network. However, such networks still exhibit fluctuations that grow linearly with the depth of the network, which may impair the training of networks with width comparable to depth. We show analytically that rectangular networks with tanh activations and weights initialized from the ensemble of orthogonal matrices have corresponding preactivation fluctuations which are independent of depth, to leading order in inverse width. Moreover, we demonstrate numerically that, at initialization, all correlators involving the neural tangent kernel (NTK) and its descendants at leading order in inverse width -- which govern the evolution of observables during training -- saturate at a depth of $\sim 20$, rather than growing without bound as in the case of Gaussian initializations. We speculate that this structure preserves finite-width feature learning while reducing overall noise, thus improving both generalization and training speed. We provide some experimental justification by relating empirical measurements of the NTK to the superior performance of deep nonlinear orthogonal networks trained under full-batch gradient descent on the MNIST and CIFAR-10 classification tasks.

A Solvable Model of Neural Scaling Laws

Large language models with a huge number of parameters, when trained on near internet-sized number of tokens, have been empirically shown to obey neural scaling laws: specifically, their performance behaves predictably as a power law in either parameters or dataset size until bottlenecked by the other resource. To understand this better, we first identify the necessary properties allowing such scaling laws to arise and then propose a statistical model -- a joint generative data model and random feature model -- that captures this neural scaling phenomenology. By solving this model in the dual limit of large training set size and large number of parameters, we gain insight into (i) the statistical structure of datasets and tasks that lead to scaling laws, (ii) the way nonlinear feature maps, such as those provided by neural networks, enable scaling laws when trained on these datasets, (iii) the optimality of the equiparameterization scaling of training sets and parameters, and (iv) whether such scaling laws can break down and how they behave when they do. Key findings are the manner in which the power laws that occur in the statistics of natural datasets are extended by nonlinear random feature maps and then translated into power-law scalings of the test loss and how the finite extent of the data's spectral power law causes the model's performance to plateau.

The Principles of Deep Learning Theory

This book develops an effective theory approach to understanding deep neural networks of practical relevance. Beginning from a first-principles component-level picture of networks, we explain how to determine an accurate description of the output of trained networks by solving layer-to-layer iteration equations and nonlinear learning dynamics. A main result is that the predictions of networks are described by nearly-Gaussian distributions, with the depth-to-width aspect ratio of the network controlling the deviations from the infinite-width Gaussian description. We explain how these effectively-deep networks learn nontrivial representations from training and more broadly analyze the mechanism of representation learning for nonlinear models. From a nearly-kernel-methods perspective, we find that the dependence of such models' predictions on the underlying learning algorithm can be expressed in a simple and universal way. To obtain these results, we develop the notion of representation group flow (RG flow) to characterize the propagation of signals through the network. By tuning networks to criticality, we give a practical solution to the exploding and vanishing gradient problem. We further explain how RG flow leads to near-universal behavior and lets us categorize networks built from different activation functions into universality classes. Altogether, we show that the depth-to-width ratio governs the effective model complexity of the ensemble of trained networks. By using information-theoretic techniques, we estimate the optimal aspect ratio at which we expect the network to be practically most useful and show how residual connections can be used to push this scale to arbitrary depths. With these tools, we can learn in detail about the inductive bias of architectures, hyperparameters, and optimizers.

SGD Implicitly Regularizes Generalization Error

We derive a simple and model-independent formula for the change in the generalization gap due to a gradient descent update. We then compare the change in the test error for stochastic gradient descent to the change in test error from an equivalent number of gradient descent updates and show explicitly that stochastic gradient descent acts to regularize generalization error by decorrelating nearby updates. These calculations depends on the details of the model only through the mean and covariance of the gradient distribution, which may be readily measured for particular models of interest. We discuss further improvements to these calculations and comment on possible implications for stochastic optimization.

Why is AI hard and Physics simple?

We discuss why AI is hard and why physics is simple. We discuss how physical intuition and the approach of theoretical physics can be brought to bear on the field of artificial intelligence and specifically machine learning. We suggest that the underlying project of machine learning and the underlying project of physics are strongly coupled through the principle of sparsity, and we call upon theoretical physicists to work on AI as physicists. As a first step in that direction, we discuss an upcoming book on the principles of deep learning theory that attempts to realize this approach.

Topological Obstructions to Autoencoding

Autoencoders have been proposed as a powerful tool for model-independent anomaly detection in high-energy physics. The operating principle is that events which do not belong to the space of training data will be reconstructed poorly, thus flagging them as anomalies. We point out that in a variety of examples of interest, the connection between large reconstruction error and anomalies is not so clear. In particular, for data sets with nontrivial topology, there will always be points that erroneously seem anomalous due to global issues. Conversely, neural networks typically have an inductive bias or prior to locally interpolate such that undersampled or rare events may be reconstructed with small error, despite actually being the desired anomalies. Taken together, these facts are in tension with the simple picture of the autoencoder as an anomaly detector. Using a series of illustrative low-dimensional examples, we show explicitly how the intrinsic and extrinsic topology of the dataset affects the behavior of an autoencoder and how this topology is manifested in the latent space representation during training. We ground this analysis in the discussion of a mock "bump hunt" in which the autoencoder fails to identify an anomalous "signal" for reasons tied to the intrinsic topology of $n$-particle phase space.

Robust Learning with Jacobian Regularization

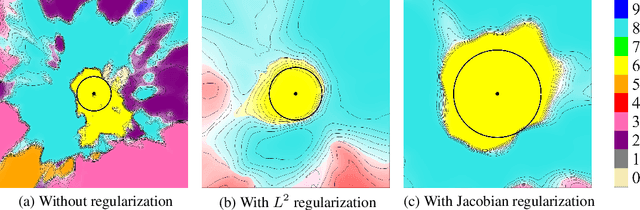
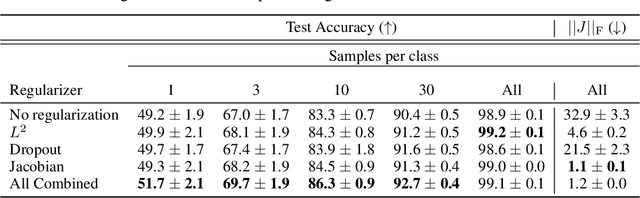
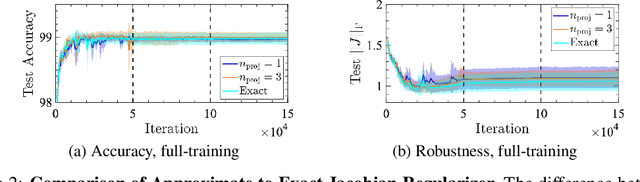
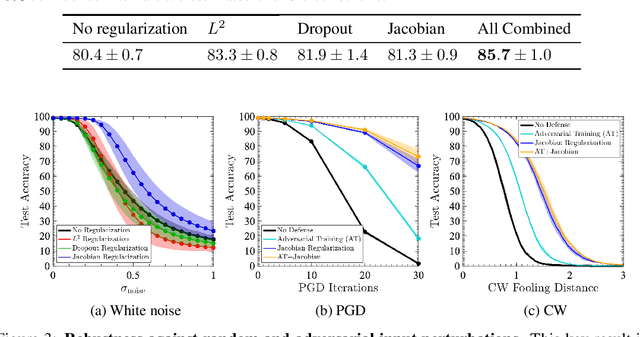
Design of reliable systems must guarantee stability against input perturbations. In machine learning, such guarantee entails preventing overfitting and ensuring robustness of models against corruption of input data. In order to maximize stability, we analyze and develop a computationally efficient implementation of Jacobian regularization that increases classification margins of neural networks. The stabilizing effect of the Jacobian regularizer leads to significant improvements in robustness, as measured against both random and adversarial input perturbations, without severely degrading generalization properties on clean data.

Gradient Descent Happens in a Tiny Subspace

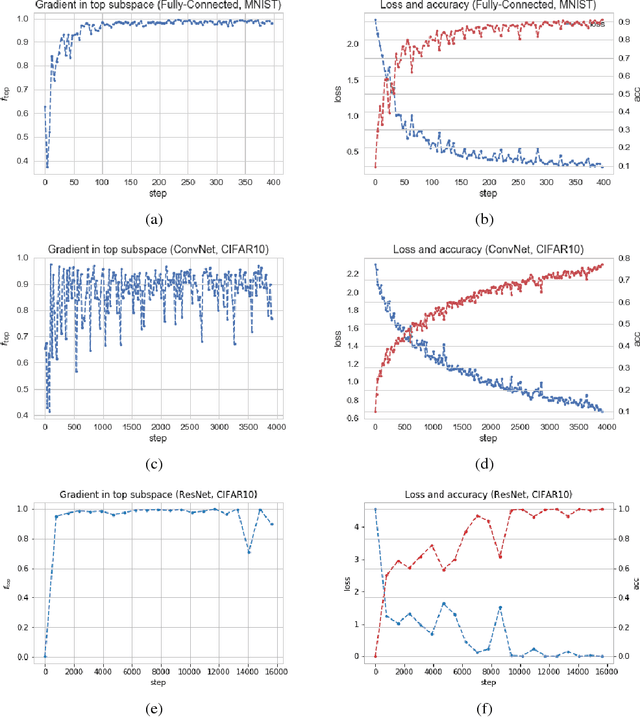
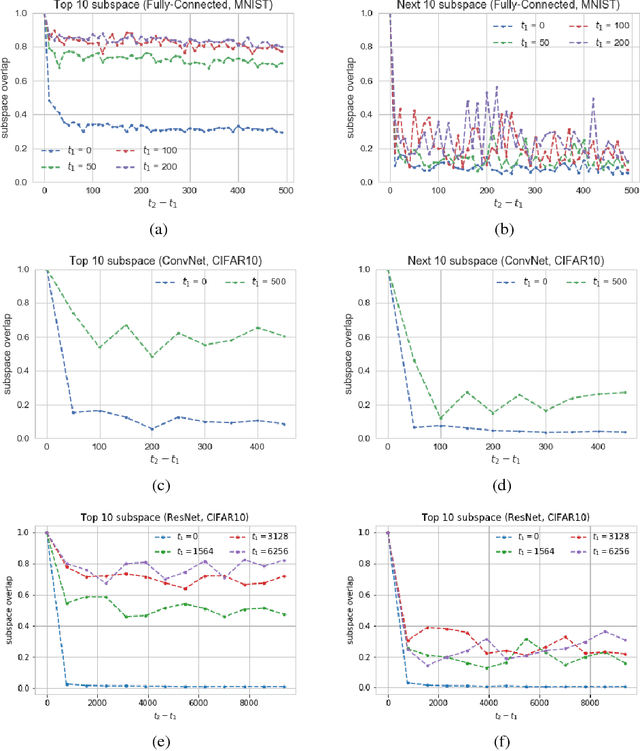
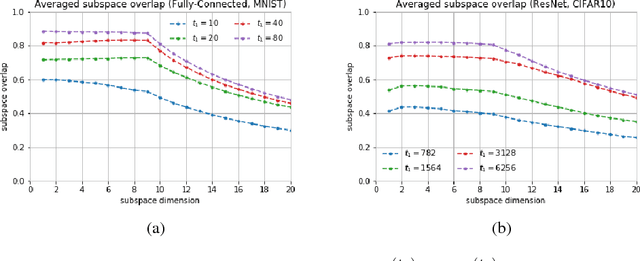
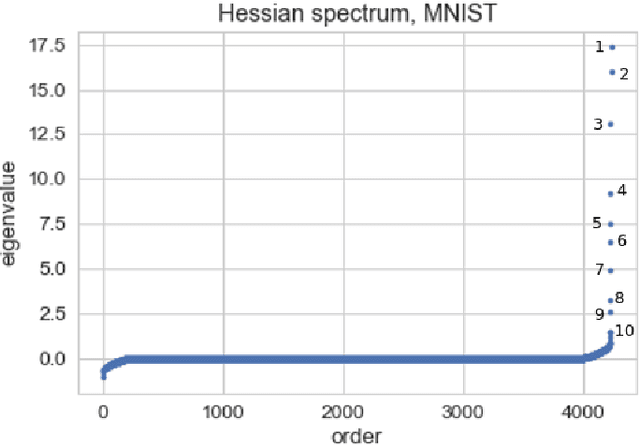
We show that in a variety of large-scale deep learning scenarios the gradient dynamically converges to a very small subspace after a short period of training. The subspace is spanned by a few top eigenvectors of the Hessian (equal to the number of classes in the dataset), and is mostly preserved over long periods of training. A simple argument then suggests that gradient descent may happen mostly in this subspace. We give an example of this effect in a solvable model of classification, and we comment on possible implications for optimization and learning.