Effective Theory of Transformers at Initialization

We perform an effective-theory analysis of forward-backward signal propagation in wide and deep Transformers, i.e., residual neural networks with multi-head self-attention blocks and multilayer perceptron blocks. This analysis suggests particular width scalings of initialization and training hyperparameters for these models. We then take up such suggestions, training Vision and Language Transformers in practical setups.

Meta-Principled Family of Hyperparameter Scaling Strategies

In this note, we first derive a one-parameter family of hyperparameter scaling strategies that interpolates between the neural-tangent scaling and mean-field/maximal-update scaling. We then calculate the scalings of dynamical observables -- network outputs, neural tangent kernels, and differentials of neural tangent kernels -- for wide and deep neural networks. These calculations in turn reveal a proper way to scale depth with width such that resultant large-scale models maintain their representation-learning ability. Finally, we observe that various infinite-width limits examined in the literature correspond to the distinct corners of the interconnected web spanned by effective theories for finite-width neural networks, with their training dynamics ranging from being weakly-coupled to being strongly-coupled.

The Principles of Deep Learning Theory

This book develops an effective theory approach to understanding deep neural networks of practical relevance. Beginning from a first-principles component-level picture of networks, we explain how to determine an accurate description of the output of trained networks by solving layer-to-layer iteration equations and nonlinear learning dynamics. A main result is that the predictions of networks are described by nearly-Gaussian distributions, with the depth-to-width aspect ratio of the network controlling the deviations from the infinite-width Gaussian description. We explain how these effectively-deep networks learn nontrivial representations from training and more broadly analyze the mechanism of representation learning for nonlinear models. From a nearly-kernel-methods perspective, we find that the dependence of such models' predictions on the underlying learning algorithm can be expressed in a simple and universal way. To obtain these results, we develop the notion of representation group flow (RG flow) to characterize the propagation of signals through the network. By tuning networks to criticality, we give a practical solution to the exploding and vanishing gradient problem. We further explain how RG flow leads to near-universal behavior and lets us categorize networks built from different activation functions into universality classes. Altogether, we show that the depth-to-width ratio governs the effective model complexity of the ensemble of trained networks. By using information-theoretic techniques, we estimate the optimal aspect ratio at which we expect the network to be practically most useful and show how residual connections can be used to push this scale to arbitrary depths. With these tools, we can learn in detail about the inductive bias of architectures, hyperparameters, and optimizers.

Non-Gaussian processes and neural networks at finite widths

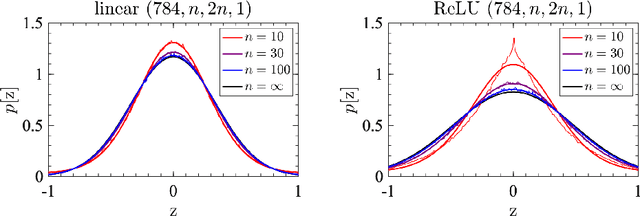
Gaussian processes are ubiquitous in nature and engineering. A case in point is a class of neural networks in the infinite-width limit, whose priors correspond to Gaussian processes. Here we perturbatively extend this correspondence to finite-width neural networks, yielding non-Gaussian processes as priors. The methodology developed herein allows us to track the flow of preactivation distributions by progressively integrating out random variables from lower to higher layers, reminiscent of renormalization-group flow. We further develop a perturbative procedure to perform Bayesian inference with weakly non-Gaussian priors.

Robust Learning with Jacobian Regularization

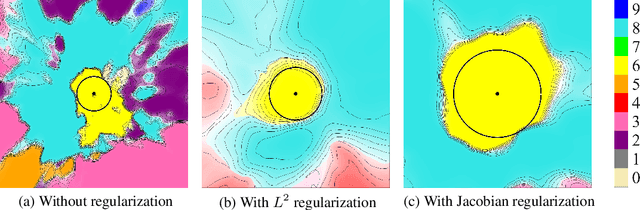
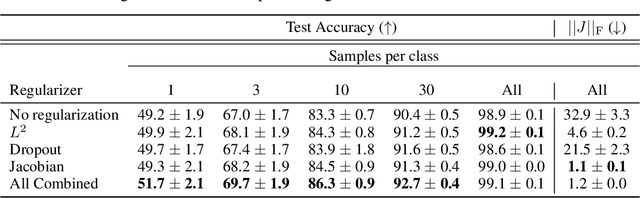
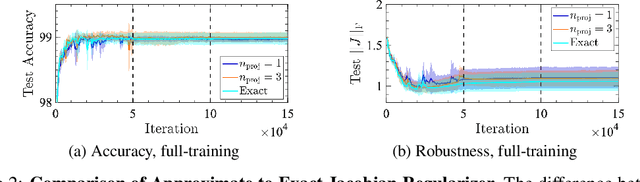
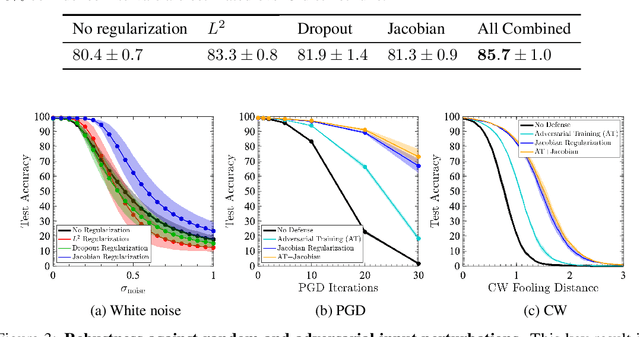
Design of reliable systems must guarantee stability against input perturbations. In machine learning, such guarantee entails preventing overfitting and ensuring robustness of models against corruption of input data. In order to maximize stability, we analyze and develop a computationally efficient implementation of Jacobian regularization that increases classification margins of neural networks. The stabilizing effect of the Jacobian regularizer leads to significant improvements in robustness, as measured against both random and adversarial input perturbations, without severely degrading generalization properties on clean data.

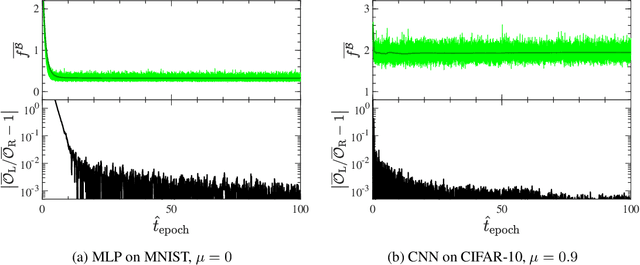
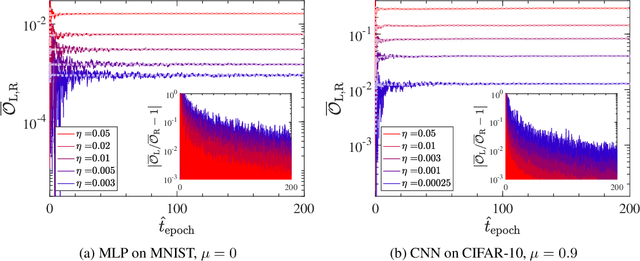
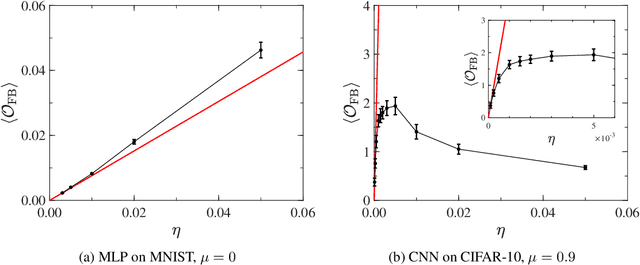
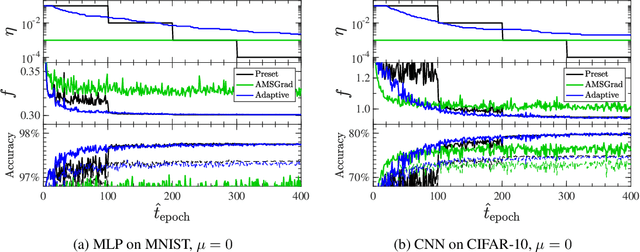
Fluctuation-dissipation relations for stochastic gradient descent

The notion of the stationary equilibrium ensemble has played a central role in statistical mechanics. In machine learning as well, training serves as generalized equilibration that drives the probability distribution of model parameters toward stationarity. Here, we derive stationary fluctuation-dissipation relations that link measurable quantities and hyperparameters in the stochastic gradient descent algorithm. These relations hold exactly for any stationary state and can in particular be used to adaptively set training schedule. We can further use the relations to efficiently extract information pertaining to a loss-function landscape such as the magnitudes of its Hessian and anharmonicity. Our claims are empirically verified.