Parameter-free Stochastic Optimization of Variationally Coherent Functions

We design and analyze an algorithm for first-order stochastic optimization of a large class of functions on $\mathbb{R}^d$. In particular, we consider the \emph{variationally coherent} functions which can be convex or non-convex. The iterates of our algorithm on variationally coherent functions converge almost surely to the global minimizer $\boldsymbol{x}^*$. Additionally, the very same algorithm with the same hyperparameters, after $T$ iterations guarantees on convex functions that the expected suboptimality gap is bounded by $\widetilde{O}(\|\boldsymbol{x}^* - \boldsymbol{x}_0\| T^{-1/2+\epsilon})$ for any $\epsilon>0$. It is the first algorithm to achieve both these properties at the same time. Also, the rate for convex functions essentially matches the performance of parameter-free algorithms. Our algorithm is an instance of the Follow The Regularized Leader algorithm with the added twist of using \emph{rescaled gradients} and time-varying linearithmic regularizers.

Bandit Multiclass Linear Classification: Efficient Algorithms for the Separable Case

We study the problem of efficient online multiclass linear classification with bandit feedback, where all examples belong to one of $K$ classes and lie in the $d$-dimensional Euclidean space. Previous works have left open the challenge of designing efficient algorithms with finite mistake bounds when the data is linearly separable by a margin $\gamma$. In this work, we take a first step towards this problem. We consider two notions of linear separability, \emph{strong} and \emph{weak}. 1. Under the strong linear separability condition, we design an efficient algorithm that achieves a near-optimal mistake bound of $O\left( K/\gamma^2 \right)$. 2. Under the more challenging weak linear separability condition, we design an efficient algorithm with a mistake bound of $\min (2^{\widetilde{O}(K \log^2 (1/\gamma))}, 2^{\widetilde{O}(\sqrt{1/\gamma} \log K)})$. Our algorithm is based on kernel Perceptron, which is inspired by the work of \citet{Klivans-Servedio-2008} on improperly learning intersection of halfspaces.

The information-theoretic value of unlabeled data in semi-supervised learning

We quantify the separation between the numbers of labeled examples required to learn in two settings: Settings with and without the knowledge of the distribution of the unlabeled data. More specifically, we prove a separation by $\Theta(\log n)$ multiplicative factor for the class of projections over the Boolean hypercube of dimension $n$. We prove that there is no separation for the class of all functions on domain of any size. Learning with the knowledge of the distribution (a.k.a. fixed-distribution learning) can be viewed as an idealized scenario of semi-supervised learning where the number of unlabeled data points is so great that the unlabeled distribution is known exactly. For this reason, we call the separation the value of unlabeled data.

Adaptive Feature Selection: Computationally Efficient Online Sparse Linear Regression under RIP

Online sparse linear regression is an online problem where an algorithm repeatedly chooses a subset of coordinates to observe in an adversarially chosen feature vector, makes a real-valued prediction, receives the true label, and incurs the squared loss. The goal is to design an online learning algorithm with sublinear regret to the best sparse linear predictor in hindsight. Without any assumptions, this problem is known to be computationally intractable. In this paper, we make the assumption that data matrix satisfies restricted isometry property, and show that this assumption leads to computationally efficient algorithms with sublinear regret for two variants of the problem. In the first variant, the true label is generated according to a sparse linear model with additive Gaussian noise. In the second, the true label is chosen adversarially.

Hardness of Online Sleeping Combinatorial Optimization Problems

We show that several online combinatorial optimization problems that admit efficient no-regret algorithms become computationally hard in the sleeping setting where a subset of actions becomes unavailable in each round. Specifically, we show that the sleeping versions of these problems are at least as hard as PAC learning DNF expressions, a long standing open problem. We show hardness for the sleeping versions of Online Shortest Paths, Online Minimum Spanning Tree, Online $k$-Subsets, Online $k$-Truncated Permutations, Online Minimum Cut, and Online Bipartite Matching. The hardness result for the sleeping version of the Online Shortest Paths problem resolves an open problem presented at COLT 2015 (Koolen et al., 2015).

Scale-Free Online Learning

We design and analyze algorithms for online linear optimization that have optimal regret and at the same time do not need to know any upper or lower bounds on the norm of the loss vectors. Our algorithms are instances of the Follow the Regularized Leader (FTRL) and Mirror Descent (MD) meta-algorithms. We achieve adaptiveness to the norms of the loss vectors by scale invariance, i.e., our algorithms make exactly the same decisions if the sequence of loss vectors is multiplied by any positive constant. The algorithm based on FTRL works for any decision set, bounded or unbounded. For unbounded decisions sets, this is the first adaptive algorithm for online linear optimization with a non-vacuous regret bound. In contrast, we show lower bounds on scale-free algorithms based on MD on unbounded domains.

Coin Betting and Parameter-Free Online Learning

In the recent years, a number of parameter-free algorithms have been developed for online linear optimization over Hilbert spaces and for learning with expert advice. These algorithms achieve optimal regret bounds that depend on the unknown competitors, without having to tune the learning rates with oracle choices. We present a new intuitive framework to design parameter-free algorithms for \emph{both} online linear optimization over Hilbert spaces and for learning with expert advice, based on reductions to betting on outcomes of adversarial coins. We instantiate it using a betting algorithm based on the Krichevsky-Trofimov estimator. The resulting algorithms are simple, with no parameters to be tuned, and they improve or match previous results in terms of regret guarantee and per-round complexity.

Toward a Classification of Finite Partial-Monitoring Games

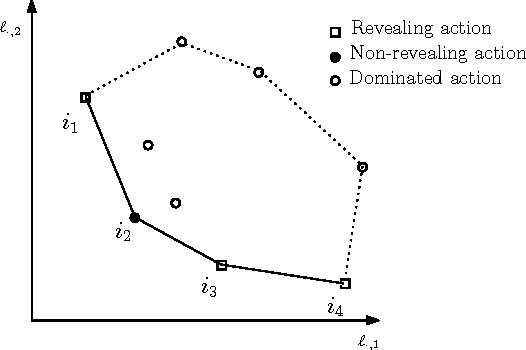
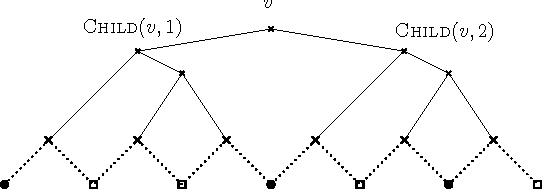
Partial-monitoring games constitute a mathematical framework for sequential decision making problems with imperfect feedback: The learner repeatedly chooses an action, opponent responds with an outcome, and then the learner suffers a loss and receives a feedback signal, both of which are fixed functions of the action and the outcome. The goal of the learner is to minimize his total cumulative loss. We make progress towards the classification of these games based on their minimax expected regret. Namely, we classify almost all games with two outcomes and finite number of actions: We show that their minimax expected regret is either zero, $\widetilde{\Theta}(\sqrt{T})$, $\Theta(T^{2/3})$, or $\Theta(T)$ and we give a simple and efficiently computable classification of these four classes of games. Our hope is that the result can serve as a stepping stone toward classifying all finite partial-monitoring games.

Estimation of Rényi Entropy and Mutual Information Based on Generalized Nearest-Neighbor Graphs

We present simple and computationally efficient nonparametric estimators of R\'enyi entropy and mutual information based on an i.i.d. sample drawn from an unknown, absolutely continuous distribution over $\R^d$. The estimators are calculated as the sum of $p$-th powers of the Euclidean lengths of the edges of the `generalized nearest-neighbor' graph of the sample and the empirical copula of the sample respectively. For the first time, we prove the almost sure consistency of these estimators and upper bounds on their rates of convergence, the latter of which under the assumption that the density underlying the sample is Lipschitz continuous. Experiments demonstrate their usefulness in independent subspace analysis.