Importance weighting without importance weights: An efficient algorithm for combinatorial semi-bandits

We propose a sample-efficient alternative for importance weighting for situations where one only has sample access to the probability distribution that generates the observations. Our new method, called Geometric Resampling (GR), is described and analyzed in the context of online combinatorial optimization under semi-bandit feedback, where a learner sequentially selects its actions from a combinatorial decision set so as to minimize its cumulative loss. In particular, we show that the well-known Follow-the-Perturbed-Leader (FPL) prediction method coupled with Geometric Resampling yields the first computationally efficient reduction from offline to online optimization in this setting. We provide a thorough theoretical analysis for the resulting algorithm, showing that its performance is on par with previous, inefficient solutions. Our main contribution is showing that, despite the relatively large variance induced by the GR procedure, our performance guarantees hold with high probability rather than only in expectation. As a side result, we also improve the best known regret bounds for FPL in online combinatorial optimization with full feedback, closing the perceived performance gap between FPL and exponential weights in this setting.

Near-Optimally Teaching the Crowd to Classify

How should we present training examples to learners to teach them classification rules? This is a natural problem when training workers for crowdsourcing labeling tasks, and is also motivated by challenges in data-driven online education. We propose a natural stochastic model of the learners, modeling them as randomly switching among hypotheses based on observed feedback. We then develop STRICT, an efficient algorithm for selecting examples to teach to workers. Our solution greedily maximizes a submodular surrogate objective function in order to select examples to show to the learners. We prove that our strategy is competitive with the optimal teaching policy. Moreover, for the special case of linear separators, we prove that an exponential reduction in error probability can be achieved. Our experiments on simulated workers as well as three real image annotation tasks on Amazon Mechanical Turk show the effectiveness of our teaching algorithm.

An efficient algorithm for learning with semi-bandit feedback

We consider the problem of online combinatorial optimization under semi-bandit feedback. The goal of the learner is to sequentially select its actions from a combinatorial decision set so as to minimize its cumulative loss. We propose a learning algorithm for this problem based on combining the Follow-the-Perturbed-Leader (FPL) prediction method with a novel loss estimation procedure called Geometric Resampling (GR). Contrary to previous solutions, the resulting algorithm can be efficiently implemented for any decision set where efficient offline combinatorial optimization is possible at all. Assuming that the elements of the decision set can be described with d-dimensional binary vectors with at most m non-zero entries, we show that the expected regret of our algorithm after T rounds is O(m sqrt(dT log d)). As a side result, we also improve the best known regret bounds for FPL in the full information setting to O(m^(3/2) sqrt(T log d)), gaining a factor of sqrt(d/m) over previous bounds for this algorithm.

Toward a Classification of Finite Partial-Monitoring Games

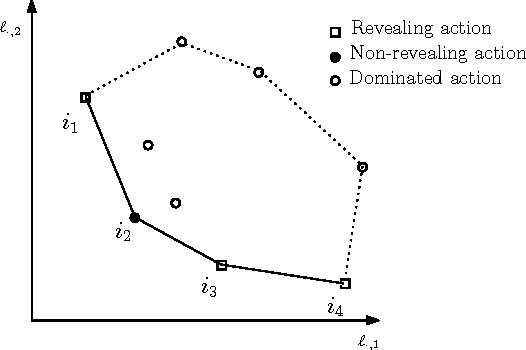
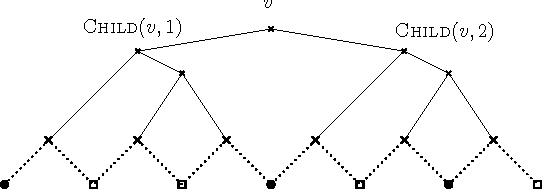
Partial-monitoring games constitute a mathematical framework for sequential decision making problems with imperfect feedback: The learner repeatedly chooses an action, opponent responds with an outcome, and then the learner suffers a loss and receives a feedback signal, both of which are fixed functions of the action and the outcome. The goal of the learner is to minimize his total cumulative loss. We make progress towards the classification of these games based on their minimax expected regret. Namely, we classify almost all games with two outcomes and finite number of actions: We show that their minimax expected regret is either zero, $\widetilde{\Theta}(\sqrt{T})$, $\Theta(T^{2/3})$, or $\Theta(T)$ and we give a simple and efficiently computable classification of these four classes of games. Our hope is that the result can serve as a stepping stone toward classifying all finite partial-monitoring games.

Non-trivial two-armed partial-monitoring games are bandits

We consider online learning in partial-monitoring games against an oblivious adversary. We show that when the number of actions available to the learner is two and the game is nontrivial then it is reducible to a bandit-like game and thus the minimax regret is $\Theta(\sqrt{T})$.