Acoustic Model Optimization over Multiple Data Sources: Merging and Valuation

Due to the rising awareness of privacy protection and the voluminous scale of speech data, it is becoming infeasible for Automatic Speech Recognition (ASR) system developers to train the acoustic model with complete data as before. For example, the data may be owned by different curators, and it is not allowed to share with others. In this paper, we propose a novel paradigm to solve salient problems plaguing the ASR field. In the first stage, multiple acoustic models are trained based upon different subsets of the complete speech data, while in the second phase, two novel algorithms are utilized to generate a high-quality acoustic model based upon those trained on data subsets. We first propose the Genetic Merge Algorithm (GMA), which is a highly specialized algorithm for optimizing acoustic models but suffers from low efficiency. We further propose the SGD-Based Optimizational Merge Algorithm (SOMA), which effectively alleviates the efficiency bottleneck of GMA and maintains superior model accuracy. Extensive experiments on public data show that the proposed methods can significantly outperform the state-of-the-art. Furthermore, we introduce Shapley Value to estimate the contribution score of the trained models, which is useful for evaluating the effectiveness of the data and providing fair incentives to their curators.

Fast and Secure Distributed Nonnegative Matrix Factorization

Nonnegative matrix factorization (NMF) has been successfully applied in several data mining tasks. Recently, there is an increasing interest in the acceleration of NMF, due to its high cost on large matrices. On the other hand, the privacy issue of NMF over federated data is worthy of attention, since NMF is prevalently applied in image and text analysis which may involve leveraging privacy data (e.g, medical image and record) across several parties (e.g., hospitals). In this paper, we study the acceleration and security problems of distributed NMF. Firstly, we propose a distributed sketched alternating nonnegative least squares (DSANLS) framework for NMF, which utilizes a matrix sketching technique to reduce the size of nonnegative least squares subproblems with a convergence guarantee. For the second problem, we show that DSANLS with modification can be adapted to the security setting, but only for one or limited iterations. Consequently, we propose four efficient distributed NMF methods in both synchronous and asynchronous settings with a security guarantee. We conduct extensive experiments on several real datasets to show the superiority of our proposed methods. The implementation of our methods is available at https://github.com/qianyuqiu79/DSANLS.

Accelerated Dual-Averaging Primal-Dual Method for Composite Convex Minimization

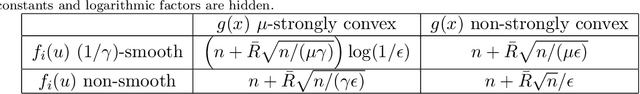
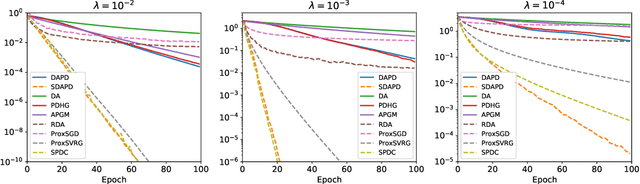
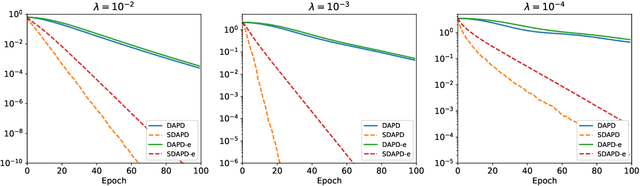
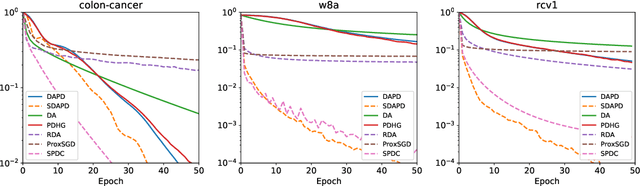
Dual averaging-type methods are widely used in industrial machine learning applications due to their ability to promoting solution structure (e.g., sparsity) efficiently. In this paper, we propose a novel accelerated dual-averaging primal-dual algorithm for minimizing a composite convex function. We also derive a stochastic version of the proposed method which solves empirical risk minimization, and its advantages on handling sparse data are demonstrated both theoretically and empirically.

Central Server Free Federated Learning over Single-sided Trust Social Networks

Federated learning has become increasingly important for modern machine learning, especially for data privacy-sensitive scenarios. Existing federated learning mostly adopts the central server-based architecture or centralized architecture. However, in many social network scenarios, centralized federated learning is not applicable (e.g., a central agent or server connecting all users may not exist, or the communication cost to the central server is not affordable). In this paper, we consider a generic setting: 1) the central server may not exist, and 2) the social network is unidirectional or of single-sided trust (i.e., user A trusts user B but user B may not trust user A). We propose a central server free federated learning algorithm, named Online Push-Sum (OPS) method, to handle this challenging but generic scenario. A rigorous regret analysis is also provided, which shows very interesting results on how users can benefit from communication with trusted users in the federated learning scenario. This work builds upon the fundamental algorithm framework and theoretical guarantees for federated learning in the generic social network scenario.

Stochastic Primal-Dual Method for Empirical Risk Minimization with $\mathcal{O}(1)$ Per-Iteration Complexity

Regularized empirical risk minimization problem with linear predictor appears frequently in machine learning. In this paper, we propose a new stochastic primal-dual method to solve this class of problems. Different from existing methods, our proposed methods only require O(1) operations in each iteration. We also develop a variance-reduction variant of the algorithm that converges linearly. Numerical experiments suggest that our methods are faster than existing ones such as proximal SGD, SVRG and SAGA on high-dimensional problems.

Barzilai-Borwein Step Size for Stochastic Gradient Descent

One of the major issues in stochastic gradient descent (SGD) methods is how to choose an appropriate step size while running the algorithm. Since the traditional line search technique does not apply for stochastic optimization algorithms, the common practice in SGD is either to use a diminishing step size, or to tune a fixed step size by hand, which can be time consuming in practice. In this paper, we propose to use the Barzilai-Borwein (BB) method to automatically compute step sizes for SGD and its variant: stochastic variance reduced gradient (SVRG) method, which leads to two algorithms: SGD-BB and SVRG-BB. We prove that SVRG-BB converges linearly for strongly convex objective functions. As a by-product, we prove the linear convergence result of SVRG with Option I proposed in [10], whose convergence result is missing in the literature. Numerical experiments on standard data sets show that the performance of SGD-BB and SVRG-BB is comparable to and sometimes even better than SGD and SVRG with best-tuned step sizes, and is superior to some advanced SGD variants.