Sequential Recommendation in Online Games with Multiple Sequences, Tasks and User Levels

Online gaming is a multi-billion-dollar industry, which is growing faster than ever before. Recommender systems (RS) for online games face unique challenges since they must fulfill players' distinct desires, at different user levels, based on their action sequences of various action types. Although many sequential RS already exist, they are mainly single-sequence, single-task, and single-user-level. In this paper, we introduce a new sequential recommendation model for multiple sequences, multiple tasks, and multiple user levels (abbreviated as M$^3$Rec) in Tencent Games platform, which can fully utilize complex data in online games. We leverage Graph Neural Network and multi-task learning to design M$^3$Rec in order to model the complex information in the heterogeneous sequential recommendation scenario of Tencent Games. We verify the effectiveness of M$^3$Rec on three online games of Tencent Games platform, in both offline and online evaluations. The results show that M$^3$Rec successfully addresses the challenges of recommendation in online games, and it generates superior recommendations compared with state-of-the-art sequential recommendation approaches.

Fast and Secure Distributed Nonnegative Matrix Factorization

Nonnegative matrix factorization (NMF) has been successfully applied in several data mining tasks. Recently, there is an increasing interest in the acceleration of NMF, due to its high cost on large matrices. On the other hand, the privacy issue of NMF over federated data is worthy of attention, since NMF is prevalently applied in image and text analysis which may involve leveraging privacy data (e.g, medical image and record) across several parties (e.g., hospitals). In this paper, we study the acceleration and security problems of distributed NMF. Firstly, we propose a distributed sketched alternating nonnegative least squares (DSANLS) framework for NMF, which utilizes a matrix sketching technique to reduce the size of nonnegative least squares subproblems with a convergence guarantee. For the second problem, we show that DSANLS with modification can be adapted to the security setting, but only for one or limited iterations. Consequently, we propose four efficient distributed NMF methods in both synchronous and asynchronous settings with a security guarantee. We conduct extensive experiments on several real datasets to show the superiority of our proposed methods. The implementation of our methods is available at https://github.com/qianyuqiu79/DSANLS.

Accelerated Dual-Averaging Primal-Dual Method for Composite Convex Minimization

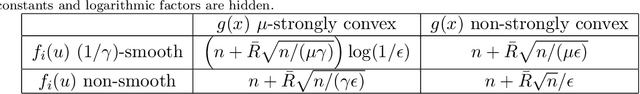
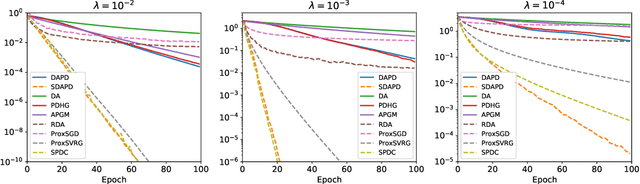
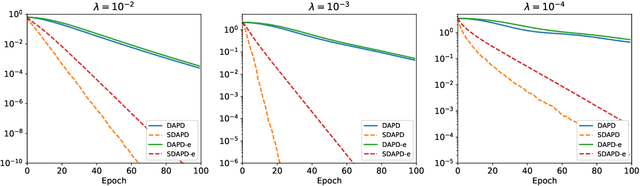
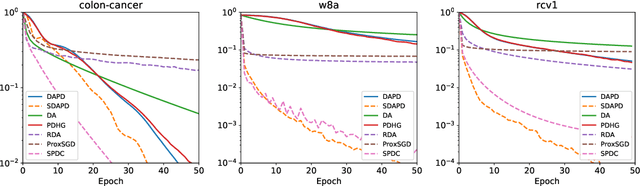
Dual averaging-type methods are widely used in industrial machine learning applications due to their ability to promoting solution structure (e.g., sparsity) efficiently. In this paper, we propose a novel accelerated dual-averaging primal-dual algorithm for minimizing a composite convex function. We also derive a stochastic version of the proposed method which solves empirical risk minimization, and its advantages on handling sparse data are demonstrated both theoretically and empirically.

An End-to-End Deep RL Framework for Task Arrangement in Crowdsourcing Platforms

In this paper, we propose a Deep Reinforcement Learning (RL) framework for task arrangement, which is a critical problem for the success of crowdsourcing platforms. Previous works conduct the personalized recommendation of tasks to workers via supervised learning methods. However, the majority of them only consider the benefit of either workers or requesters independently. In addition, they cannot handle the dynamic environment and may produce sub-optimal results. To address these issues, we utilize Deep Q-Network (DQN), an RL-based method combined with a neural network to estimate the expected long-term return of recommending a task. DQN inherently considers the immediate and future reward simultaneously and can be updated in real-time to deal with evolving data and dynamic changes. Furthermore, we design two DQNs that capture the benefit of both workers and requesters and maximize the profit of the platform. To learn value functions in DQN effectively, we also propose novel state representations, carefully design the computation of Q values, and predict transition probabilities and future states. Experiments on synthetic and real datasets demonstrate the superior performance of our framework.

Barzilai-Borwein Step Size for Stochastic Gradient Descent

One of the major issues in stochastic gradient descent (SGD) methods is how to choose an appropriate step size while running the algorithm. Since the traditional line search technique does not apply for stochastic optimization algorithms, the common practice in SGD is either to use a diminishing step size, or to tune a fixed step size by hand, which can be time consuming in practice. In this paper, we propose to use the Barzilai-Borwein (BB) method to automatically compute step sizes for SGD and its variant: stochastic variance reduced gradient (SVRG) method, which leads to two algorithms: SGD-BB and SVRG-BB. We prove that SVRG-BB converges linearly for strongly convex objective functions. As a by-product, we prove the linear convergence result of SVRG with Option I proposed in [10], whose convergence result is missing in the literature. Numerical experiments on standard data sets show that the performance of SGD-BB and SVRG-BB is comparable to and sometimes even better than SGD and SVRG with best-tuned step sizes, and is superior to some advanced SGD variants.