Accelerated Dual-Averaging Primal-Dual Method for Composite Convex Minimization
Paper and Code
Jan 15, 2020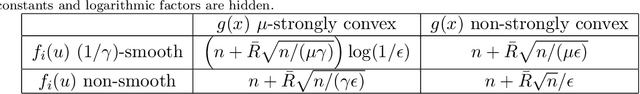
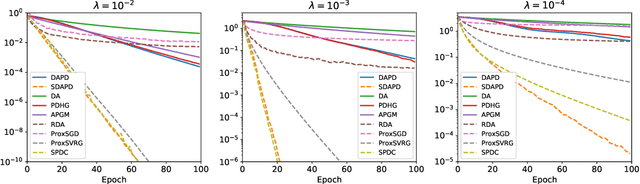
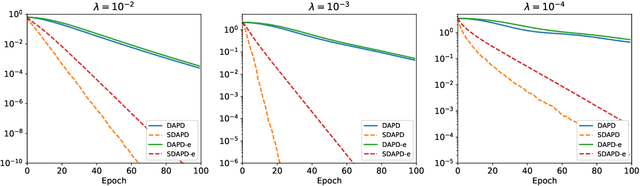
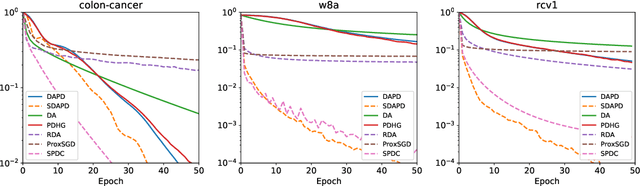
Dual averaging-type methods are widely used in industrial machine learning applications due to their ability to promoting solution structure (e.g., sparsity) efficiently. In this paper, we propose a novel accelerated dual-averaging primal-dual algorithm for minimizing a composite convex function. We also derive a stochastic version of the proposed method which solves empirical risk minimization, and its advantages on handling sparse data are demonstrated both theoretically and empirically.
* Optimization Methods and Software 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge