Neuro-Symbolic Data Generation for Math Reasoning

A critical question about Large Language Models (LLMs) is whether their apparent deficiency in mathematical reasoning is inherent, or merely a result of insufficient exposure to high-quality mathematical data. To explore this, we developed an automated method for generating high-quality, supervised mathematical datasets. The method carefully mutates existing math problems, ensuring both diversity and validity of the newly generated problems. This is achieved by a neuro-symbolic data generation framework combining the intuitive informalization strengths of LLMs, and the precise symbolic reasoning of math solvers along with projected Markov chain Monte Carlo sampling in the highly-irregular symbolic space. Empirical experiments demonstrate the high quality of data generated by the proposed method, and that the LLMs, specifically LLaMA-2 and Mistral, when realigned with the generated data, surpass their state-of-the-art counterparts.

Executing Arithmetic: Fine-Tuning Large Language Models as Turing Machines

Large Language Models (LLMs) have demonstrated remarkable capabilities across a wide range of natural language processing and reasoning tasks. However, their performance in the foundational domain of arithmetic remains unsatisfactory. When dealing with arithmetic tasks, LLMs often memorize specific examples rather than learning the underlying computational logic, limiting their ability to generalize to new problems. In this paper, we propose a Composable Arithmetic Execution Framework (CAEF) that enables LLMs to learn to execute step-by-step computations by emulating Turing Machines, thereby gaining a genuine understanding of computational logic. Moreover, the proposed framework is highly scalable, allowing composing learned operators to significantly reduce the difficulty of learning complex operators. In our evaluation, CAEF achieves nearly 100% accuracy across seven common mathematical operations on the LLaMA 3.1-8B model, effectively supporting computations involving operands with up to 100 digits, a level where GPT-4o falls short noticeably in some settings.

Softened Symbol Grounding for Neuro-symbolic Systems

Neuro-symbolic learning generally consists of two separated worlds, i.e., neural network training and symbolic constraint solving, whose success hinges on symbol grounding, a fundamental problem in AI. This paper presents a novel, softened symbol grounding process, bridging the gap between the two worlds, and resulting in an effective and efficient neuro-symbolic learning framework. Technically, the framework features (1) modeling of symbol solution states as a Boltzmann distribution, which avoids expensive state searching and facilitates mutually beneficial interactions between network training and symbolic reasoning;(2) a new MCMC technique leveraging projection and SMT solvers, which efficiently samples from disconnected symbol solution spaces; (3) an annealing mechanism that can escape from %being trapped into sub-optimal symbol groundings. Experiments with three representative neuro symbolic learning tasks demonstrate that, owining to its superior symbol grounding capability, our framework successfully solves problems well beyond the frontier of the existing proposals.

Operational Calibration: Debugging Confidence Errors for DNNs in the Field

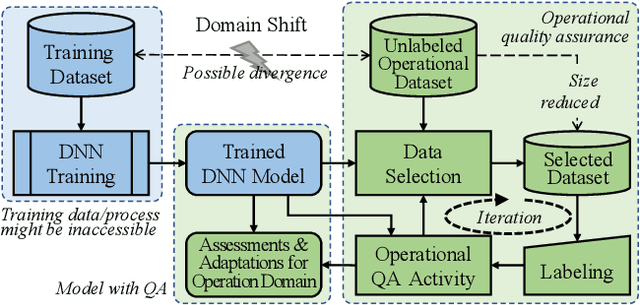
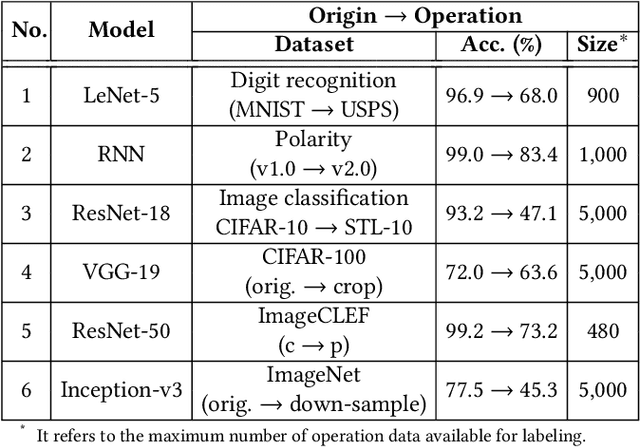
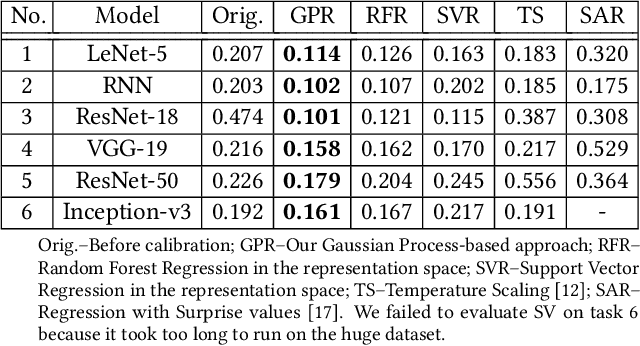
Trained DNN models are increasingly adopted as integral parts of software systems. However, they are often over-confident, especially in practical operation domains where slight divergence from their training data almost always exists. To minimize the loss due to inaccurate confidence, operational calibration, i.e., calibrating the confidence function of a DNN classifier against its operation domain, becomes a necessary debugging step in the engineering of the whole system. Operational calibration is difficult considering the limited budget of labeling operation data and the weak interpretability of DNN models. We propose a Bayesian approach to operational calibration that gradually corrects the confidence given by the model under calibration with a small number of labeled operational data deliberately selected from a larger set of unlabeled operational data. Exploiting the locality of the learned representation of the DNN model and modeling the calibration as Gaussian Process Regression, the approach achieves impressive efficacy and efficiency. Comprehensive experiments with various practical data sets and DNN models show that it significantly outperformed alternative methods, and in some difficult tasks it eliminated about 71% to 97% high-confidence errors with only about 10% of the minimal amount of labeled operation data needed for practical learning techniques to barely work.

Boosting Operational DNN Testing Efficiency through Conditioning

With the increasing adoption of Deep Neural Network (DNN) models as integral parts of software systems, efficient operational testing of DNNs is much in demand to ensure these models' actual performance in field conditions. A challenge is that the testing often needs to produce precise results with a very limited budget for labeling data collected in field. Viewing software testing as a practice of reliability estimation through statistical sampling, we re-interpret the idea behind conventional structural coverages as conditioning for variance reduction. With this insight we propose an efficient DNN testing method based on the conditioning on the representation learned by the DNN model under testing. The representation is defined by the probability distribution of the output of neurons in the last hidden layer of the model. To sample from this high dimensional distribution in which the operational data are sparsely distributed, we design an algorithm leveraging cross entropy minimization. Experiments with various DNN models and datasets were conducted to evaluate the general efficiency of the approach. The results show that, compared with simple random sampling, this approach requires only about a half of labeled inputs to achieve the same level of precision.