MIPI 2024 Challenge on Few-shot RAW Image Denoising: Methods and Results

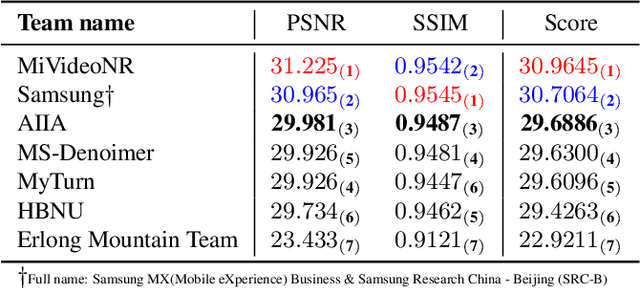
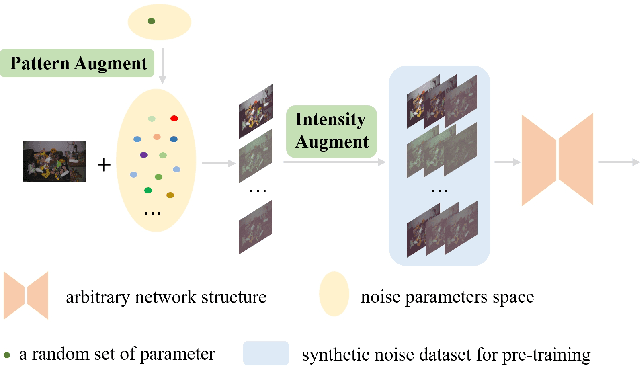
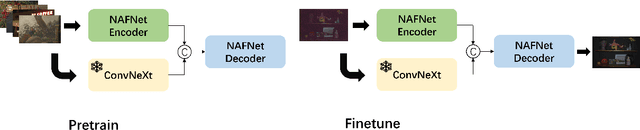
The increasing demand for computational photography and imaging on mobile platforms has led to the widespread development and integration of advanced image sensors with novel algorithms in camera systems. However, the scarcity of high-quality data for research and the rare opportunity for in-depth exchange of views from industry and academia constrain the development of mobile intelligent photography and imaging (MIPI). Building on the achievements of the previous MIPI Workshops held at ECCV 2022 and CVPR 2023, we introduce our third MIPI challenge including three tracks focusing on novel image sensors and imaging algorithms. In this paper, we summarize and review the Few-shot RAW Image Denoising track on MIPI 2024. In total, 165 participants were successfully registered, and 7 teams submitted results in the final testing phase. The developed solutions in this challenge achieved state-of-the-art erformance on Few-shot RAW Image Denoising. More details of this challenge and the link to the dataset can be found at https://mipichallenge.org/MIPI2024.

Deep RAW Image Super-Resolution. A NTIRE 2024 Challenge Survey

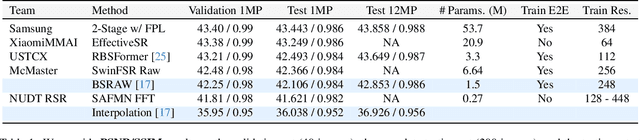
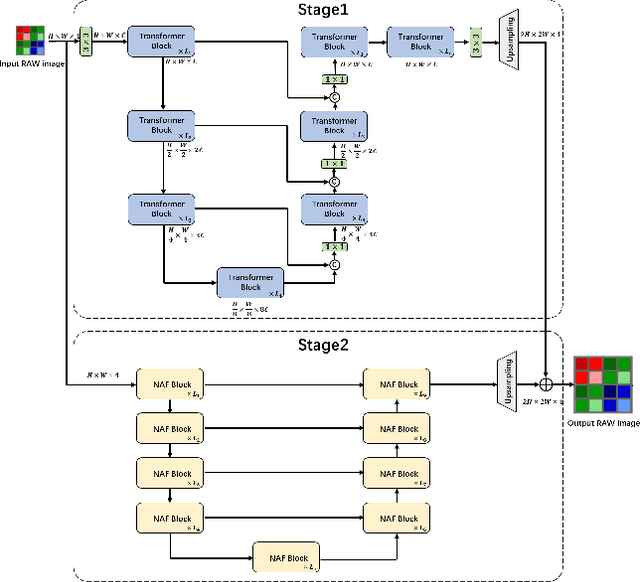
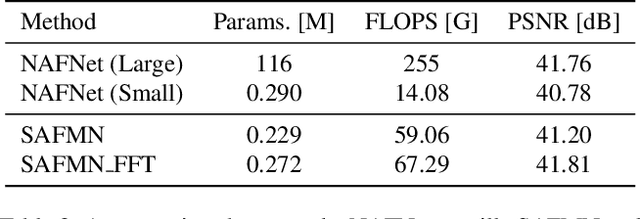
This paper reviews the NTIRE 2024 RAW Image Super-Resolution Challenge, highlighting the proposed solutions and results. New methods for RAW Super-Resolution could be essential in modern Image Signal Processing (ISP) pipelines, however, this problem is not as explored as in the RGB domain. Th goal of this challenge is to upscale RAW Bayer images by 2x, considering unknown degradations such as noise and blur. In the challenge, a total of 230 participants registered, and 45 submitted results during thee challenge period. The performance of the top-5 submissions is reviewed and provided here as a gauge for the current state-of-the-art in RAW Image Super-Resolution.

Learning Stochastic Dynamics with Statistics-Informed Neural Network

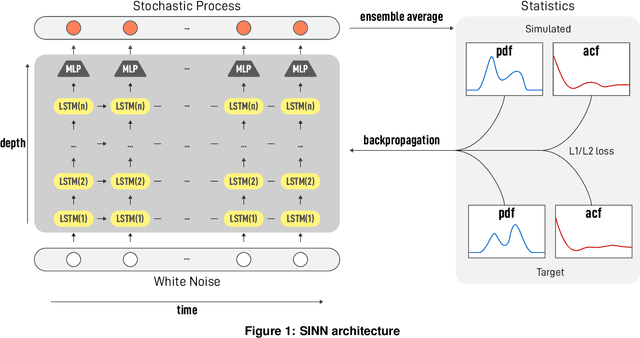
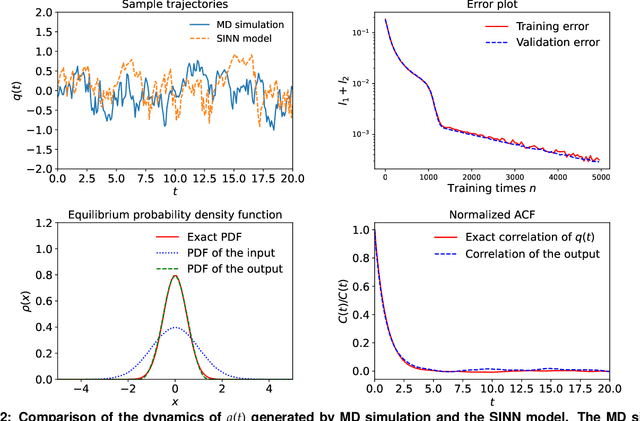
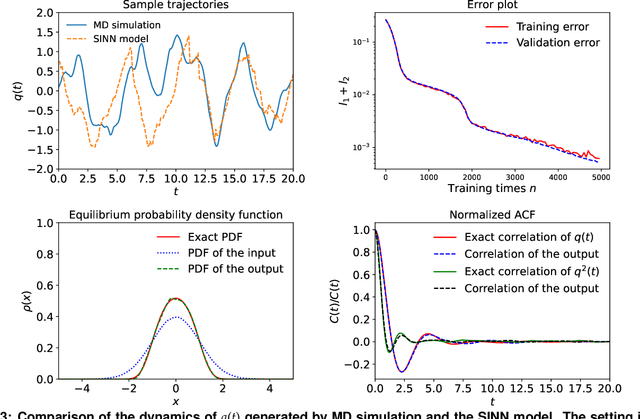
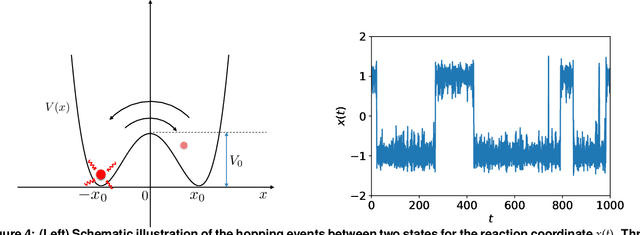
We introduce a machine-learning framework named statistics-informed neural network (SINN) for learning stochastic dynamics from data. This new architecture was theoretically inspired by a universal approximation theorem for stochastic systems introduced in this paper and the projection-operator formalism for stochastic modeling. We devise mechanisms for training the neural network model to reproduce the correct \emph{statistical} behavior of a target stochastic process. Numerical simulation results demonstrate that a well-trained SINN can reliably approximate both Markovian and non-Markovian stochastic dynamics. We demonstrate the applicability of SINN to model transition dynamics. Furthermore, we show that the obtained reduced-order model can be trained on temporally coarse-grained data and hence is well suited for rare-event simulations.