Learning Stochastic Dynamics with Statistics-Informed Neural Network

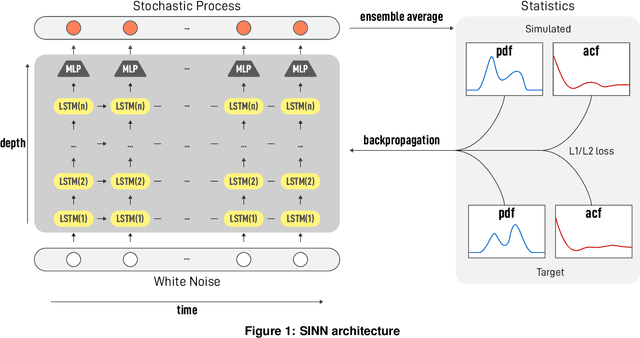
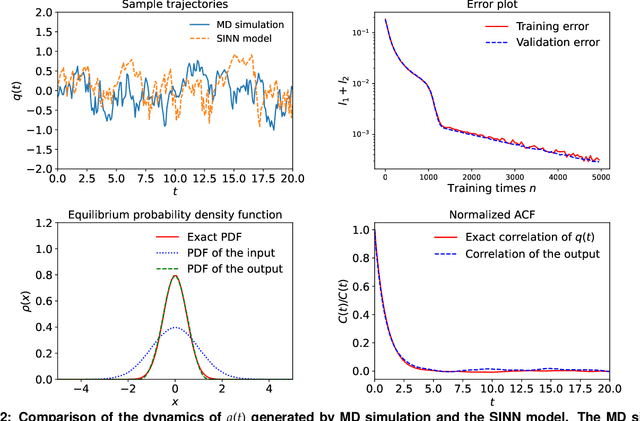
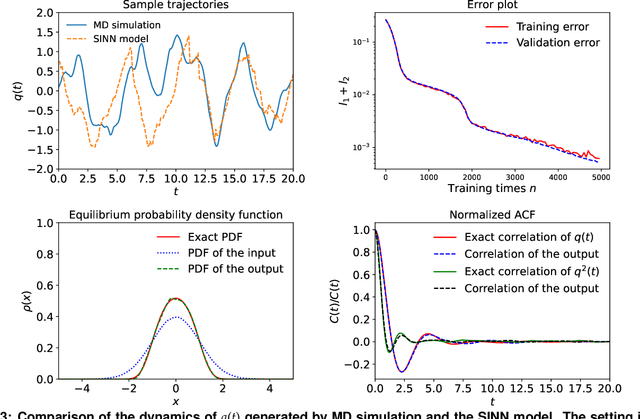
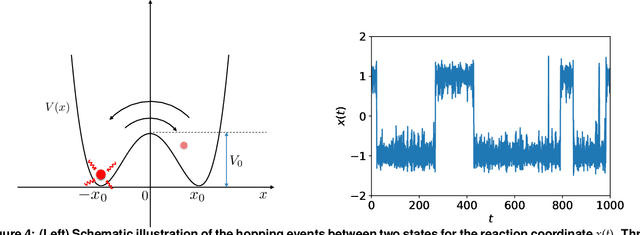
We introduce a machine-learning framework named statistics-informed neural network (SINN) for learning stochastic dynamics from data. This new architecture was theoretically inspired by a universal approximation theorem for stochastic systems introduced in this paper and the projection-operator formalism for stochastic modeling. We devise mechanisms for training the neural network model to reproduce the correct \emph{statistical} behavior of a target stochastic process. Numerical simulation results demonstrate that a well-trained SINN can reliably approximate both Markovian and non-Markovian stochastic dynamics. We demonstrate the applicability of SINN to model transition dynamics. Furthermore, we show that the obtained reduced-order model can be trained on temporally coarse-grained data and hence is well suited for rare-event simulations.