Ce Ju
SPD Learning for Covariance-Based Neuroimaging Analysis: Perspectives, Methods, and Challenges
Apr 26, 2025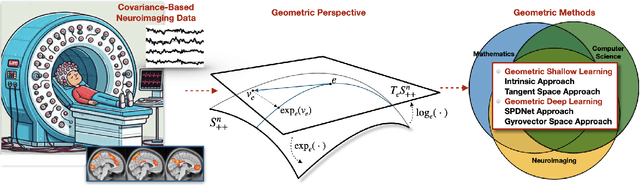

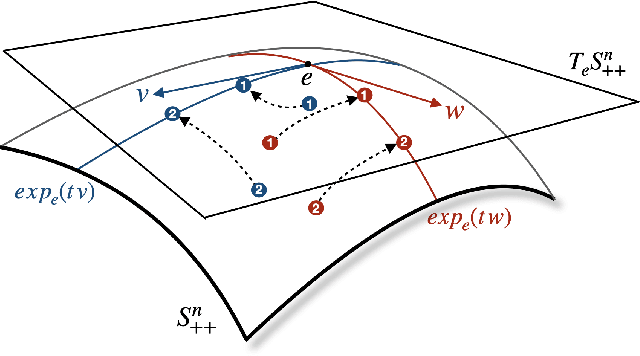
Abstract:Neuroimaging provides a critical framework for characterizing brain activity by quantifying connectivity patterns and functional architecture across modalities. While modern machine learning has significantly advanced our understanding of neural processing mechanisms through these datasets, decoding task-specific signatures must contend with inherent neuroimaging constraints, for example, low signal-to-noise ratios in raw electrophysiological recordings, cross-session non-stationarity, and limited sample sizes. This review focuses on machine learning approaches for covariance-based neuroimaging data, where often symmetric positive definite (SPD) matrices under full-rank conditions encode inter-channel relationships. By equipping the space of SPD matrices with Riemannian metrics (e.g., affine-invariant or log-Euclidean), their space forms a Riemannian manifold enabling geometric analysis. We unify methodologies operating on this manifold under the SPD learning framework, which systematically leverages the SPD manifold's geometry to process covariance features, thereby advancing brain imaging analytics.
Score-based Data Generation for EEG Spatial Covariance Matrices: Towards Boosting BCI Performance
Feb 22, 2023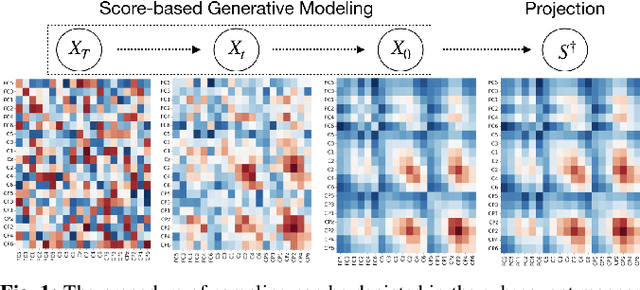
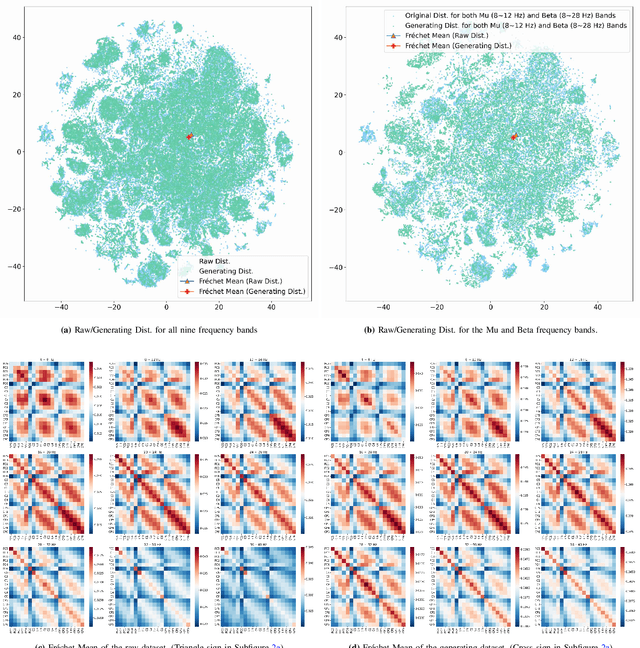
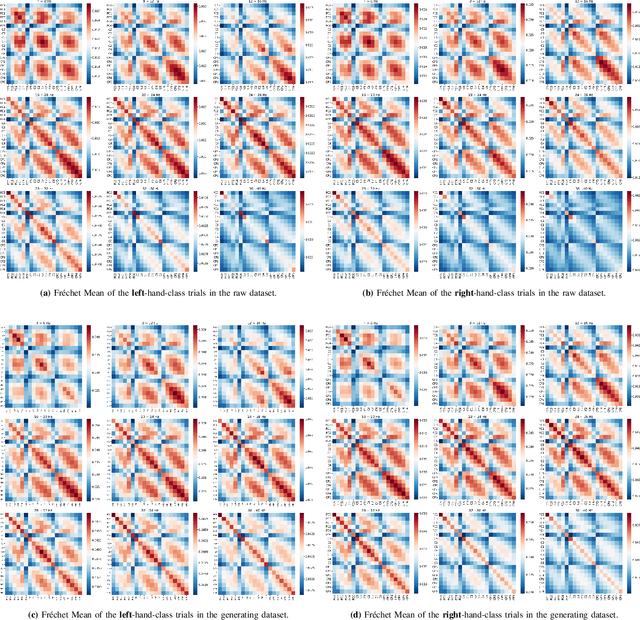
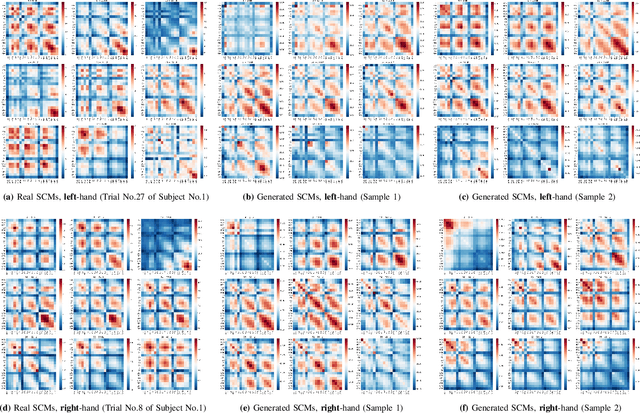
Abstract:The efficacy of Electroencephalogram (EEG) classifiers can be augmented by increasing the quantity of available data. In the case of geometric deep learning classifiers, the input consists of spatial covariance matrices derived from EEGs. To synthesize these spatial covariance matrices, we propose a generative modeling technique based on state-of-the-art score-based models. The quality of generated samples is evaluated through visual and quantitative assessments using a binary-class motor imagery dataset. The exceptional pixel-level resolution of these generative samples highlights the formidable capacity of score-based generative modeling. Additionally, the center (Frechet mean) of the generated samples aligns with neurophysiological evidence that event-related desynchronization and synchronization occur on electrodes C3 and C4 within the Mu and Beta frequency bands during motor imagery processing. The quantitative evaluation revealed that 84.3% of the generated samples could be accurately predicted by a pre-trained classifier and an improvement of up to 8.7% in the average accuracy over ten runs for a specific test subject in a holdout experiment.
Graph Neural Networks on SPD Manifolds for Motor Imagery Classification: A Perspective from the Time-Frequency Analysis
Oct 25, 2022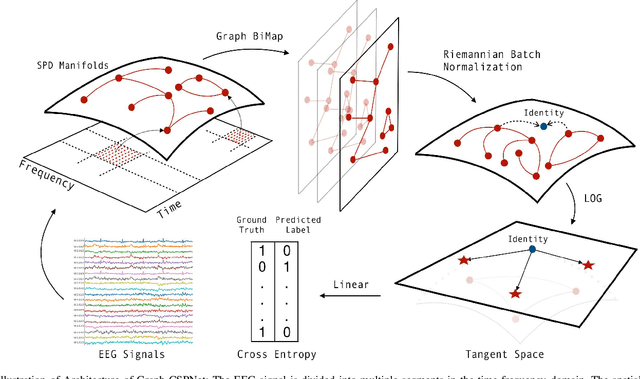

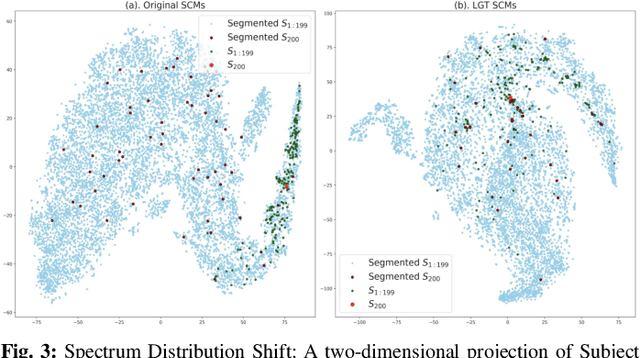

Abstract:Motor imagery (MI) classification is one of the most widely-concern research topics in Electroencephalography (EEG)-based brain-computer interfaces (BCIs) with extensive industry value. The MI-EEG classifiers' tendency has changed fundamentally over the past twenty years, while classifiers' performance is gradually increasing. In particular, owing to the need for characterizing signals' non-Euclidean inherence, the first geometric deep learning (GDL) framework, Tensor-CSPNet, has recently emerged in the BCI study. In essence, Tensor-CSPNet is a deep learning-based classifier on the second-order statistics of EEGs. In contrast to the first-order statistics, using these second-order statistics is the classical treatment of EEG signals, and the discriminative information contained in these second-order statistics is adequate for MI-EEG classification. In this study, we present another GDL classifier for MI-EEG classification called Graph-CSPNet, using graph-based techniques to simultaneously characterize the EEG signals in both the time and frequency domains. It is realized from the perspective of the time-frequency analysis that profoundly influences signal processing and BCI studies. Contrary to Tensor-CSPNet, the architecture of Graph-CSPNet is further simplified with more flexibility to cope with variable time-frequency resolution for signal segmentation to capture the localized fluctuations. In the experiments, Graph-CSPNet is evaluated on subject-specific scenarios from two well-used MI-EEG datasets and produces near-optimal classification accuracies.
Tensor-CSPNet: A Novel Geometric Deep Learning Framework for Motor Imagery Classification
Feb 05, 2022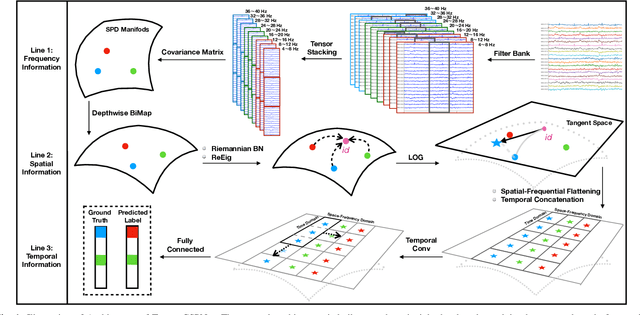
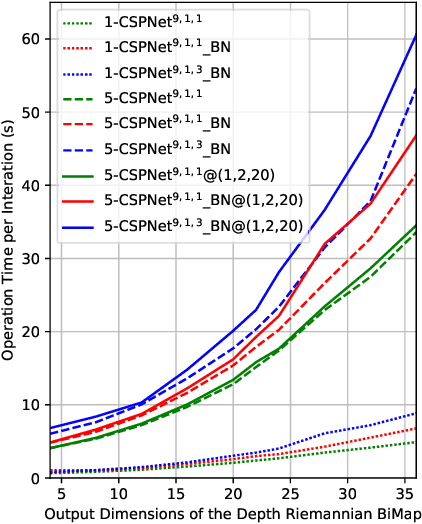
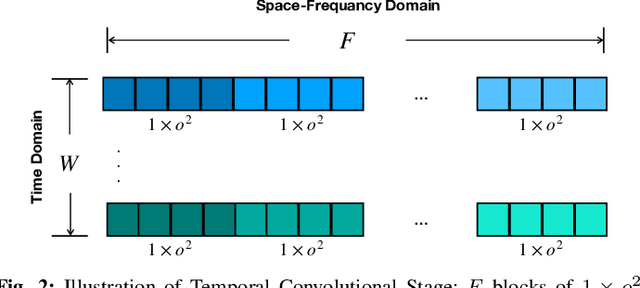

Abstract:Deep learning (DL) has been widely investigated in a vast majority of applications in electroencephalography (EEG)-based brain-computer interfaces (BCIs), especially for motor imagery (MI) classification in the past five years. The mainstream DL methodology for the MI-EEG classification exploits the temporospatial patterns of EEG signals using convolutional neural networks (CNNs), which have been particularly successful in visual images. However, since the statistical characteristics of visual images may not benefit EEG signals, a natural question that arises is whether there exists an alternative network architecture despite CNNs to extract features for the MI-EEG classification. To address this question, we propose a novel geometric deep learning (GDL) framework called Tensor-CSPNet to characterize EEG signals on symmetric positive definite (SPD) manifolds and exploit the temporo-spatio-frequential patterns using deep neural networks on SPD manifolds. Meanwhile, many experiences of successful MI-EEG classifiers have been integrated into the Tensor-CSPNet framework to make it more efficient. In the experiments, Tensor-CSPNet attains or slightly outperforms the current state-of-the-art performance on the cross-validation and holdout scenarios of two MI-EEG datasets. The visualization and interpretability analyses also exhibit its validity for the MI-EEG classification. To conclude, we provide a feasible answer to the question by generalizing the previous DL methodologies on SPD manifolds, which indicates the start of a specific class from the GDL methodology for the MI-EEG classification.
Deep Optimal Transport on SPD Manifolds for Domain Adaptation
Jan 15, 2022



Abstract:The domain adaption (DA) problem on symmetric positive definite (SPD) manifolds has raised interest in the machine learning community because of the growing potential for the SPD-matrix representations across many non-stationary applicable scenarios. This paper generalizes the joint distribution adaption (JDA) to align the source and target domains on SPD manifolds and proposes a deep network architecture, Deep Optimal Transport (DOT), using the generalized JDA and the existing deep network architectures on SPD manifolds. The specific architecture in DOT enables it to learn an approximate optimal transport (OT) solution to the DA problems on SPD manifolds. In the experiments, DOT exhibits a 2.32% and 2.92% increase on the average accuracy in two highly non-stationary cross-session scenarios in brain-computer interfaces (BCIs), respectively. The visualizational results of the source and target domains before and after the transformation also demonstrate the validity of DOT.
Ternary Hashing
Mar 19, 2021
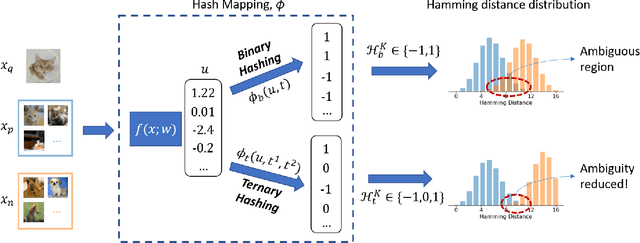
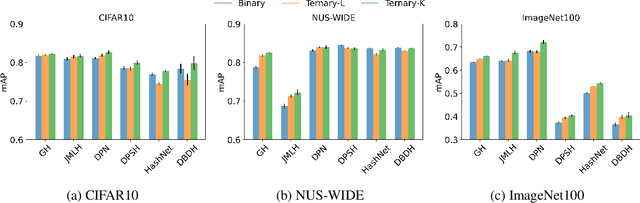
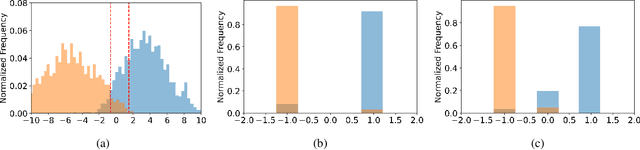
Abstract:This paper proposes a novel ternary hash encoding for learning to hash methods, which provides a principled more efficient coding scheme with performances better than those of the state-of-the-art binary hashing counterparts. Two kinds of axiomatic ternary logic, Kleene logic and {\L}ukasiewicz logic are adopted to calculate the Ternary Hamming Distance (THD) for both the learning/encoding and testing/querying phases. Our work demonstrates that, with an efficient implementation of ternary logic on standard binary machines, the proposed ternary hashing is compared favorably to the binary hashing methods with consistent improvements of retrieval mean average precision (mAP) ranging from 1\% to 5.9\% as shown in CIFAR10, NUS-WIDE and ImageNet100 datasets.
Rethinking Uncertainty in Deep Learning: Whether and How it Improves Robustness
Nov 27, 2020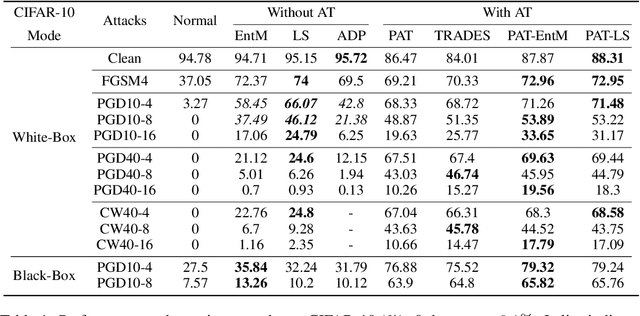
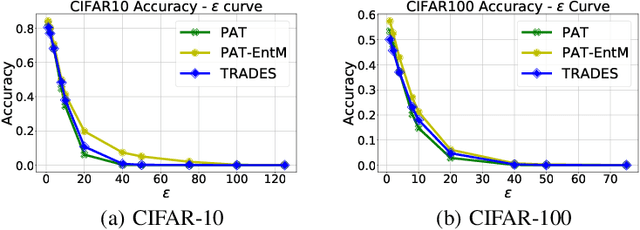
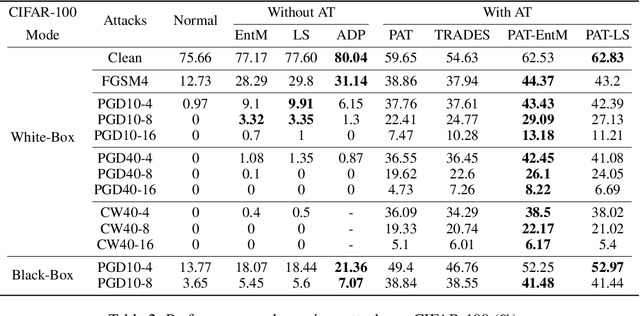

Abstract:Deep neural networks (DNNs) are known to be prone to adversarial attacks, for which many remedies are proposed. While adversarial training (AT) is regarded as the most robust defense, it suffers from poor performance both on clean examples and under other types of attacks, e.g. attacks with larger perturbations. Meanwhile, regularizers that encourage uncertain outputs, such as entropy maximization (EntM) and label smoothing (LS) can maintain accuracy on clean examples and improve performance under weak attacks, yet their ability to defend against strong attacks is still in doubt. In this paper, we revisit uncertainty promotion regularizers, including EntM and LS, in the field of adversarial learning. We show that EntM and LS alone provide robustness only under small perturbations. Contrarily, we show that uncertainty promotion regularizers complement AT in a principled manner, consistently improving performance on both clean examples and under various attacks, especially attacks with large perturbations. We further analyze how uncertainty promotion regularizers enhance the performance of AT from the perspective of Jacobian matrices $\nabla_X f(X;\theta)$, and find out that EntM effectively shrinks the norm of Jacobian matrices and hence promotes robustness.
Geometric Foundations of Data Reduction
Aug 16, 2020
Abstract:The purpose of this paper is to write a complete survey of the (spectral) manifold learning methods and nonlinear dimensionality reduction (NLDR) in data reduction. The first two NLDR methods in history were respectively published in Science in 2000 in which they solve the similar reduction problem of high-dimensional data endowed with the intrinsic nonlinear structure. The intrinsic nonlinear structure is always interpreted as a concept in manifolds from geometry and topology in theoretical mathematics by computer scientists and theoretical physicists. In 2001, the concept of Manifold Learning first appears as an NLDR method called Laplacian Eigenmaps purposed by Belkin and Niyogi. In the typical manifold learning setup, the data set, also called the observation set, is distributed on or near a low dimensional manifold $M$ embedded in $\mathbb{R}^D$, which yields that each observation has a $D$-dimensional representation. The goal of (spectral) manifold learning is to reduce these observations as a compact lower-dimensional representation based on the geometric information. The reduction procedure is called the (spectral) manifold learning method. In this paper, we derive each (spectral) manifold learning method with the matrix and operator representation, and we then discuss the convergence behavior of each method in a geometric uniform language. Hence, we name the survey Geometric Foundations of Data Reduction.
Privacy Threats Against Federated Matrix Factorization
Jul 03, 2020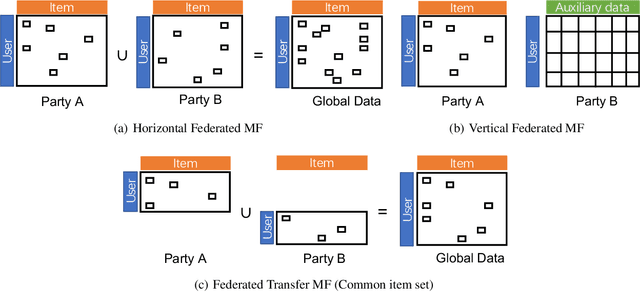
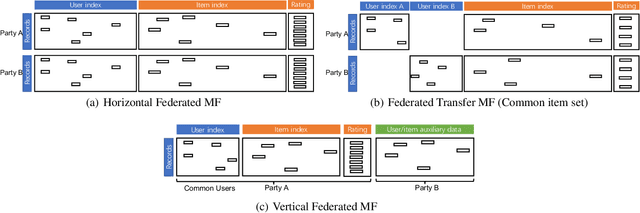
Abstract:Matrix Factorization has been very successful in practical recommendation applications and e-commerce. Due to data shortage and stringent regulations, it can be hard to collect sufficient data to build performant recommender systems for a single company. Federated learning provides the possibility to bridge the data silos and build machine learning models without compromising privacy and security. Participants sharing common users or items collaboratively build a model over data from all the participants. There have been some works exploring the application of federated learning to recommender systems and the privacy issues in collaborative filtering systems. However, the privacy threats in federated matrix factorization are not studied. In this paper, we categorize federated matrix factorization into three types based on the partition of feature space and analyze privacy threats against each type of federated matrix factorization model. We also discuss privacy-preserving approaches. As far as we are aware, this is the first study of privacy threats of the matrix factorization method in the federated learning framework.
Rethinking Privacy Preserving Deep Learning: How to Evaluate and Thwart Privacy Attacks
Jun 23, 2020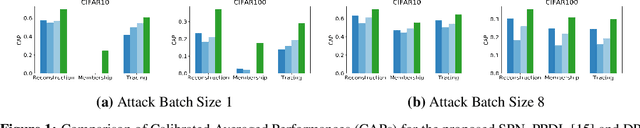

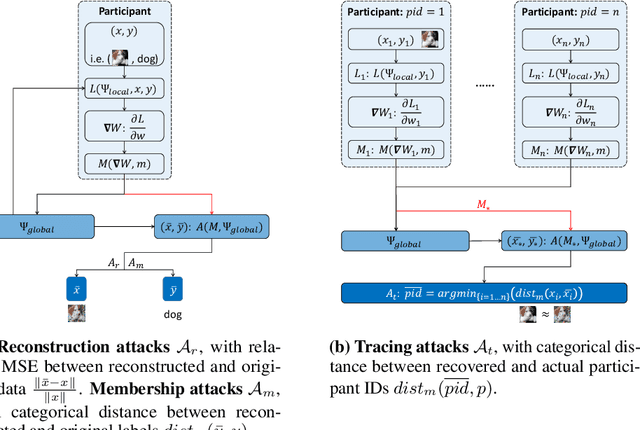
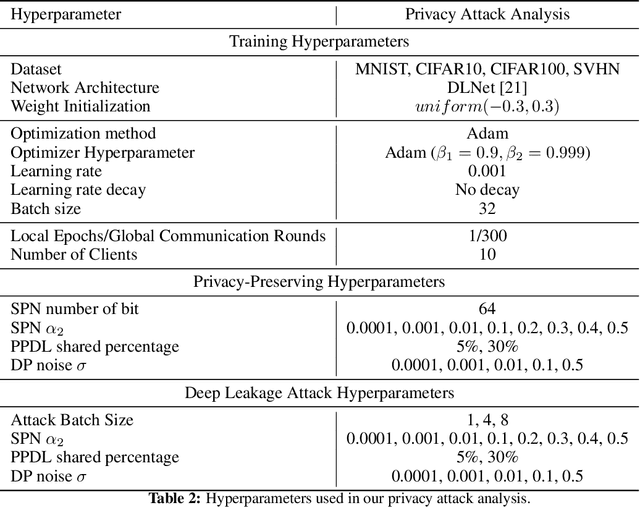
Abstract:This paper investigates capabilities of Privacy-Preserving Deep Learning (PPDL) mechanisms against various forms of privacy attacks. First, we propose to quantitatively measure the trade-off between model accuracy and privacy losses incurred by reconstruction, tracing and membership attacks. Second, we formulate reconstruction attacks as solving a noisy system of linear equations, and prove that attacks are guaranteed to be defeated if condition (2) is unfulfilled. Third, based on theoretical analysis, a novel Secret Polarization Network (SPN) is proposed to thwart privacy attacks, which pose serious challenges to existing PPDL methods. Extensive experiments showed that model accuracies are improved on average by 5-20% compared with baseline mechanisms, in regimes where data privacy are satisfactorily protected.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge