Tensor-CSPNet: A Novel Geometric Deep Learning Framework for Motor Imagery Classification

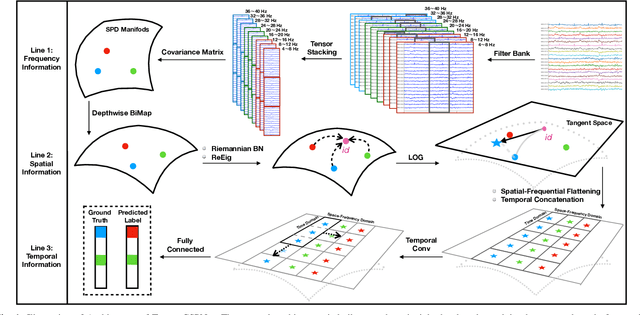
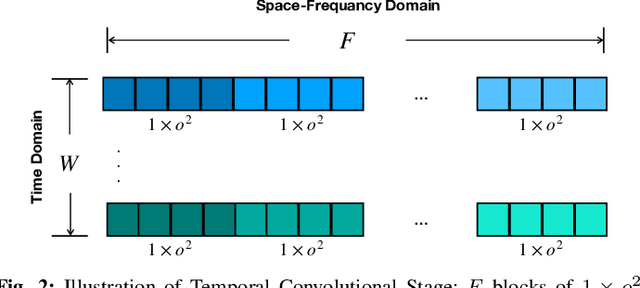
Deep learning (DL) has been widely investigated in a vast majority of applications in electroencephalography (EEG)-based brain-computer interfaces (BCIs), especially for motor imagery (MI) classification in the past five years. The mainstream DL methodology for the MI-EEG classification exploits the temporospatial patterns of EEG signals using convolutional neural networks (CNNs), which have been particularly successful in visual images. However, since the statistical characteristics of visual images may not benefit EEG signals, a natural question that arises is whether there exists an alternative network architecture despite CNNs to extract features for the MI-EEG classification. To address this question, we propose a novel geometric deep learning (GDL) framework called Tensor-CSPNet to characterize EEG signals on symmetric positive definite (SPD) manifolds and exploit the temporo-spatio-frequential patterns using deep neural networks on SPD manifolds. Meanwhile, many experiences of successful MI-EEG classifiers have been integrated into the Tensor-CSPNet framework to make it more efficient. In the experiments, Tensor-CSPNet attains or slightly outperforms the current state-of-the-art performance on the cross-validation and holdout scenarios of two MI-EEG datasets. The visualization and interpretability analyses also exhibit its validity for the MI-EEG classification. To conclude, we provide a feasible answer to the question by generalizing the previous DL methodologies on SPD manifolds, which indicates the start of a specific class from the GDL methodology for the MI-EEG classification.