Caihua Chen
LEDiT: Your Length-Extrapolatable Diffusion Transformer without Positional Encoding
Mar 07, 2025Abstract:Diffusion transformers(DiTs) struggle to generate images at resolutions higher than their training resolutions. The primary obstacle is that the explicit positional encodings(PE), such as RoPE, need extrapolation which degrades performance when the inference resolution differs from training. In this paper, we propose a Length-Extrapolatable Diffusion Transformer(LEDiT), a simple yet powerful architecture to overcome this limitation. LEDiT needs no explicit PEs, thereby avoiding extrapolation. The key innovations of LEDiT are introducing causal attention to implicitly impart global positional information to tokens, while enhancing locality to precisely distinguish adjacent tokens. Experiments on 256x256 and 512x512 ImageNet show that LEDiT can scale the inference resolution to 512x512 and 1024x1024, respectively, while achieving better image quality compared to current state-of-the-art length extrapolation methods(NTK-aware, YaRN). Moreover, LEDiT achieves strong extrapolation performance with just 100K steps of fine-tuning on a pretrained DiT, demonstrating its potential for integration into existing text-to-image DiTs. Project page: https://shenzhang2145.github.io/ledit/
Fast Epigraphical Projection-based Incremental Algorithms for Wasserstein Distributionally Robust Support Vector Machine
Oct 24, 2020

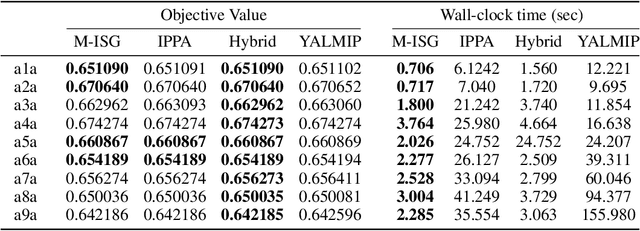

Abstract:Wasserstein \textbf{D}istributionally \textbf{R}obust \textbf{O}ptimization (DRO) is concerned with finding decisions that perform well on data that are drawn from the worst-case probability distribution within a Wasserstein ball centered at a certain nominal distribution. In recent years, it has been shown that various DRO formulations of learning models admit tractable convex reformulations. However, most existing works propose to solve these convex reformulations by general-purpose solvers, which are not well-suited for tackling large-scale problems. In this paper, we focus on a family of Wasserstein distributionally robust support vector machine (DRSVM) problems and propose two novel epigraphical projection-based incremental algorithms to solve them. The updates in each iteration of these algorithms can be computed in a highly efficient manner. Moreover, we show that the DRSVM problems considered in this paper satisfy a H\"olderian growth condition with explicitly determined growth exponents. Consequently, we are able to establish the convergence rates of the proposed incremental algorithms. Our numerical results indicate that the proposed methods are orders of magnitude faster than the state-of-the-art, and the performance gap grows considerably as the problem size increases.
On Isometry Robustness of Deep 3D Point Cloud Models under Adversarial Attacks
Mar 10, 2020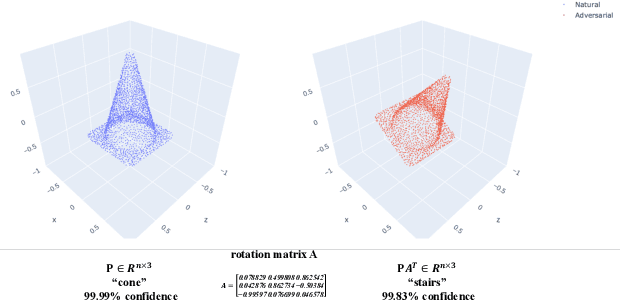
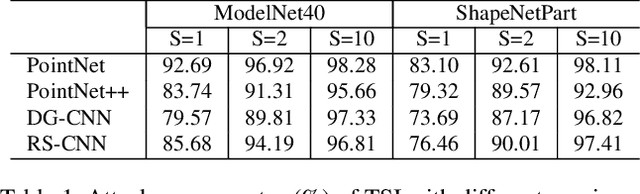
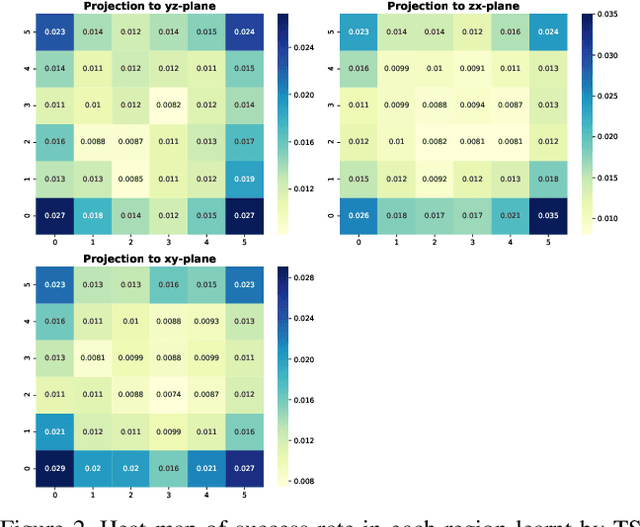
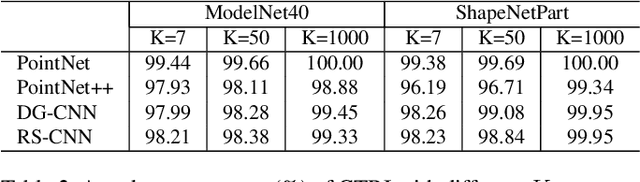
Abstract:While deep learning in 3D domain has achieved revolutionary performance in many tasks, the robustness of these models has not been sufficiently studied or explored. Regarding the 3D adversarial samples, most existing works focus on manipulation of local points, which may fail to invoke the global geometry properties, like robustness under linear projection that preserves the Euclidean distance, i.e., isometry. In this work, we show that existing state-of-the-art deep 3D models are extremely vulnerable to isometry transformations. Armed with the Thompson Sampling, we develop a black-box attack with success rate over 95% on ModelNet40 data set. Incorporating with the Restricted Isometry Property, we propose a novel framework of white-box attack on top of spectral norm based perturbation. In contrast to previous works, our adversarial samples are experimentally shown to be strongly transferable. Evaluated on a sequence of prevailing 3D models, our white-box attack achieves success rates from 98.88% to 100%. It maintains a successful attack rate over 95% even within an imperceptible rotation range $[\pm 2.81^{\circ}]$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge