Fast Epigraphical Projection-based Incremental Algorithms for Wasserstein Distributionally Robust Support Vector Machine
Paper and Code
Oct 24, 2020

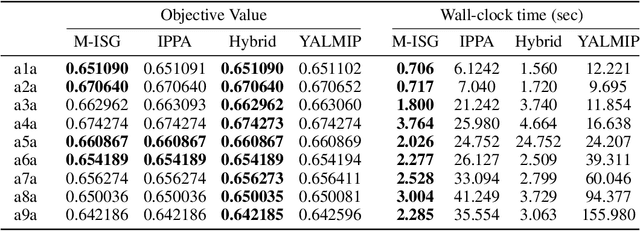

Wasserstein \textbf{D}istributionally \textbf{R}obust \textbf{O}ptimization (DRO) is concerned with finding decisions that perform well on data that are drawn from the worst-case probability distribution within a Wasserstein ball centered at a certain nominal distribution. In recent years, it has been shown that various DRO formulations of learning models admit tractable convex reformulations. However, most existing works propose to solve these convex reformulations by general-purpose solvers, which are not well-suited for tackling large-scale problems. In this paper, we focus on a family of Wasserstein distributionally robust support vector machine (DRSVM) problems and propose two novel epigraphical projection-based incremental algorithms to solve them. The updates in each iteration of these algorithms can be computed in a highly efficient manner. Moreover, we show that the DRSVM problems considered in this paper satisfy a H\"olderian growth condition with explicitly determined growth exponents. Consequently, we are able to establish the convergence rates of the proposed incremental algorithms. Our numerical results indicate that the proposed methods are orders of magnitude faster than the state-of-the-art, and the performance gap grows considerably as the problem size increases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge