Predicting Risk of Developing Diabetic Retinopathy using Deep Learning

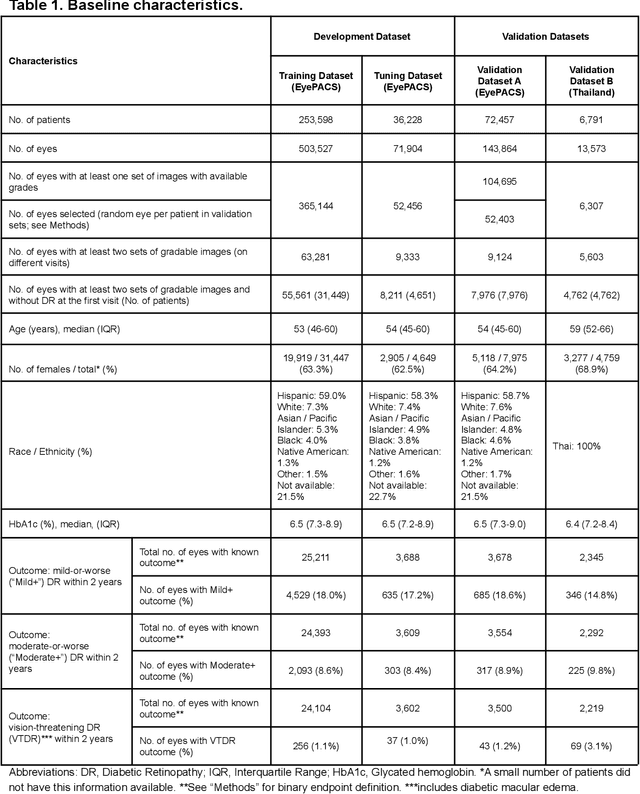
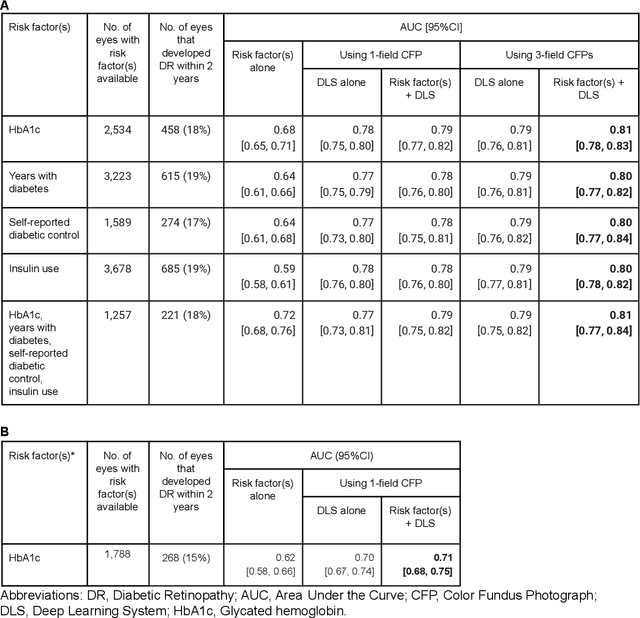
Diabetic retinopathy (DR) screening is instrumental in preventing blindness, but faces a scaling challenge as the number of diabetic patients rises. Risk stratification for the development of DR may help optimize screening intervals to reduce costs while improving vision-related outcomes. We created and validated two versions of a deep learning system (DLS) to predict the development of mild-or-worse ("Mild+") DR in diabetic patients undergoing DR screening. The two versions used either three-fields or a single field of color fundus photographs (CFPs) as input. The training set was derived from 575,431 eyes, of which 28,899 had known 2-year outcome, and the remaining were used to augment the training process via multi-task learning. Validation was performed on both an internal validation set (set A; 7,976 eyes; 3,678 with known outcome) and an external validation set (set B; 4,762 eyes; 2,345 with known outcome). For predicting 2-year development of DR, the 3-field DLS had an area under the receiver operating characteristic curve (AUC) of 0.79 (95%CI, 0.78-0.81) on validation set A. On validation set B (which contained only a single field), the 1-field DLS's AUC was 0.70 (95%CI, 0.67-0.74). The DLS was prognostic even after adjusting for available risk factors (p<0.001). When added to the risk factors, the 3-field DLS improved the AUC from 0.72 (95%CI, 0.68-0.76) to 0.81 (95%CI, 0.77-0.84) in validation set A, and the 1-field DLS improved the AUC from 0.62 (95%CI, 0.58-0.66) to 0.71 (95%CI, 0.68-0.75) in validation set B. The DLSs in this study identified prognostic information for DR development from CFPs. This information is independent of and more informative than the available risk factors.

Deep Learning to Assess Glaucoma Risk and Associated Features in Fundus Images

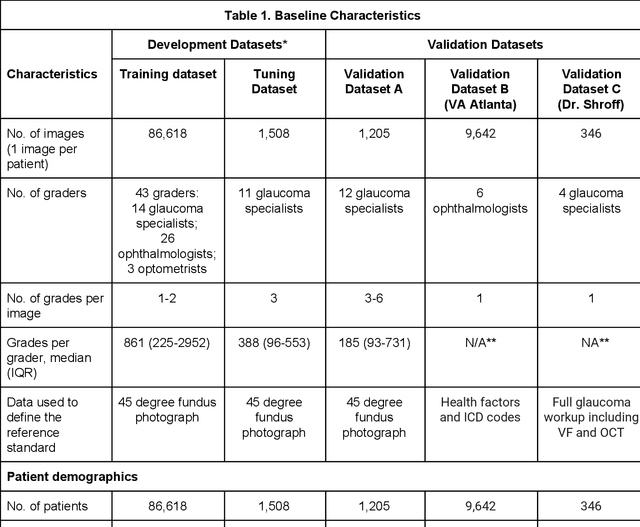
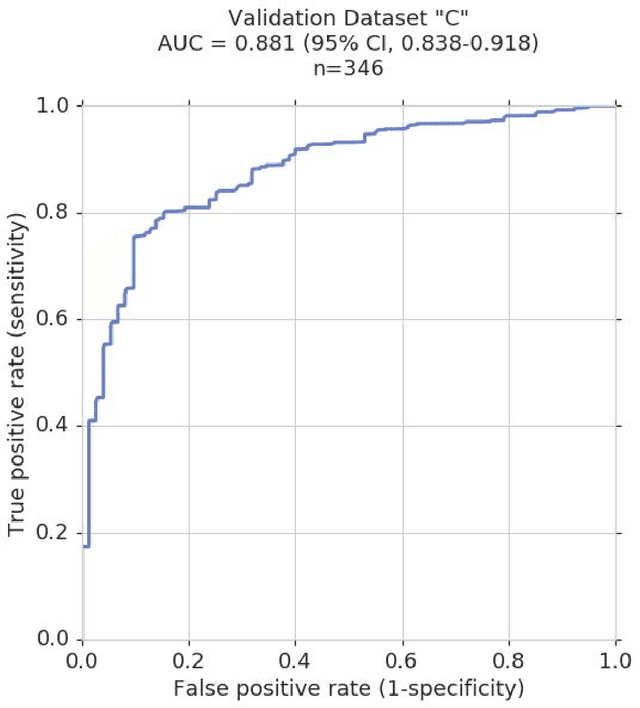
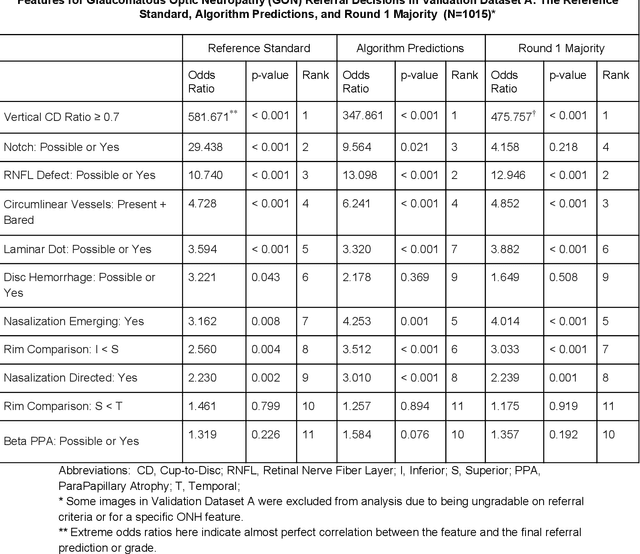
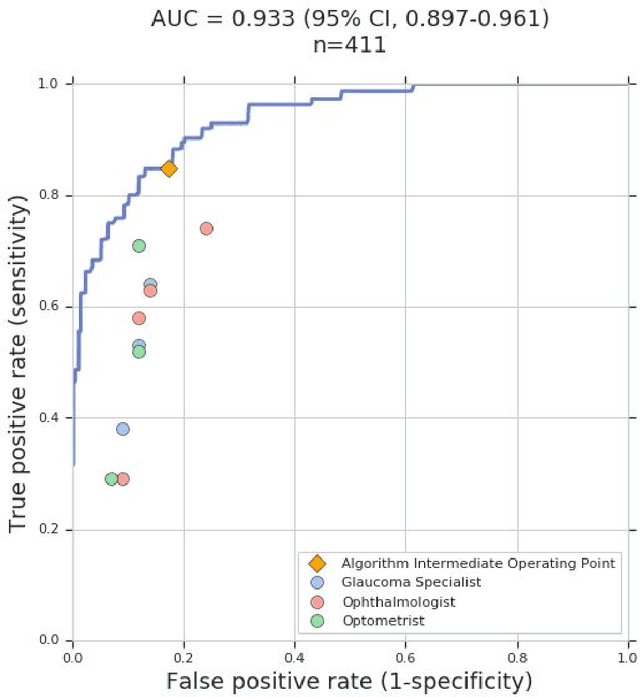
Glaucoma is the leading cause of preventable, irreversible blindness world-wide. The disease can remain asymptomatic until severe, and an estimated 50%-90% of people with glaucoma remain undiagnosed. Thus, glaucoma screening is recommended for early detection and treatment. A cost-effective tool to detect glaucoma could expand healthcare access to a much larger patient population, but such a tool is currently unavailable. We trained a deep learning (DL) algorithm using a retrospective dataset of 58,033 images, assessed for gradability, glaucomatous optic nerve head (ONH) features, and referable glaucoma risk. The resultant algorithm was validated using 2 separate datasets. For referable glaucoma risk, the algorithm had an AUC of 0.940 (95%CI, 0.922-0.955) in validation dataset "A" (1,205 images, 1 image/patient; 19% referable where images were adjudicated by panels of fellowship-trained glaucoma specialists) and 0.858 (95% CI, 0.836-0.878) in validation dataset "B" (17,593 images from 9,643 patients; 9.2% referable where images were from the Atlanta Veterans Affairs Eye Clinic diabetic teleretinal screening program using clinical referral decisions as the reference standard). Additionally, we found that the presence of vertical cup-to-disc ratio >= 0.7, neuroretinal rim notching, retinal nerve fiber layer defect, and bared circumlinear vessels contributed most to referable glaucoma risk assessment by both glaucoma specialists and the algorithm. Algorithm AUCs ranged between 0.608-0.977 for glaucomatous ONH features. The DL algorithm was significantly more sensitive than 6 of 10 graders, including 2 of 3 glaucoma specialists, with comparable or higher specificity relative to all graders. A DL algorithm trained on fundus images alone can detect referable glaucoma risk with higher sensitivity and comparable specificity to eye care providers.

Compressed Sensing using Generative Models

The goal of compressed sensing is to estimate a vector from an underdetermined system of noisy linear measurements, by making use of prior knowledge on the structure of vectors in the relevant domain. For almost all results in this literature, the structure is represented by sparsity in a well-chosen basis. We show how to achieve guarantees similar to standard compressed sensing but without employing sparsity at all. Instead, we suppose that vectors lie near the range of a generative model $G: \mathbb{R}^k \to \mathbb{R}^n$. Our main theorem is that, if $G$ is $L$-Lipschitz, then roughly $O(k \log L)$ random Gaussian measurements suffice for an $\ell_2/\ell_2$ recovery guarantee. We demonstrate our results using generative models from published variational autoencoder and generative adversarial networks. Our method can use $5$-$10$x fewer measurements than Lasso for the same accuracy.

Graphical RNN Models

Many time series are generated by a set of entities that interact with one another over time. This paper introduces a broad, flexible framework to learn from multiple inter-dependent time series generated by such entities. Our framework explicitly models the entities and their interactions through time. It achieves this by building on the capabilities of Recurrent Neural Networks, while also offering several ways to incorporate domain knowledge/constraints into the model architecture. The capabilities of our approach are showcased through an application to weather prediction, which shows gains over strong baselines.