Leveraging Distributional Bias for Reactive Collision Avoidance under Uncertainty: A Kernel Embedding Approach

Many commodity sensors that measure the robot and dynamic obstacle's state have non-Gaussian noise characteristics. Yet, many current approaches treat the underlying-uncertainty in motion and perception as Gaussian, primarily to ensure computational tractability. On the other hand, existing planners working with non-Gaussian uncertainty do not shed light on leveraging distributional characteristics of motion and perception noise, such as bias for efficient collision avoidance. This paper fills this gap by interpreting reactive collision avoidance as a distribution matching problem between the collision constraint violations and Dirac Delta distribution. To ensure fast reactivity in the planner, we embed each distribution in Reproducing Kernel Hilbert Space and reformulate the distribution matching as minimizing the Maximum Mean Discrepancy (MMD) between the two distributions. We show that evaluating the MMD for a given control input boils down to just matrix-matrix products. We leverage this insight to develop a simple control sampling approach for reactive collision avoidance with dynamic and uncertain obstacles. We advance the state-of-the-art in two respects. First, we conduct an extensive empirical study to show that our planner can infer distributional bias from sample-level information. Consequently, it uses this insight to guide the robot to good homotopy. We also highlight how a Gaussian approximation of the underlying uncertainty can lose the bias estimate and guide the robot to unfavorable states with a high collision probability. Second, we show tangible comparative advantages of the proposed distribution matching approach for collision avoidance with previous non-parametric and Gaussian approximated methods of reactive collision avoidance.

Non Holonomic Collision Avoidance of Dynamic Obstacles under Non-Parametric Uncertainty: A Hilbert Space Approach

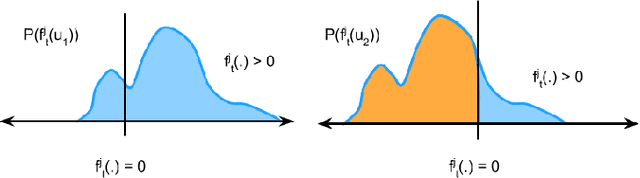
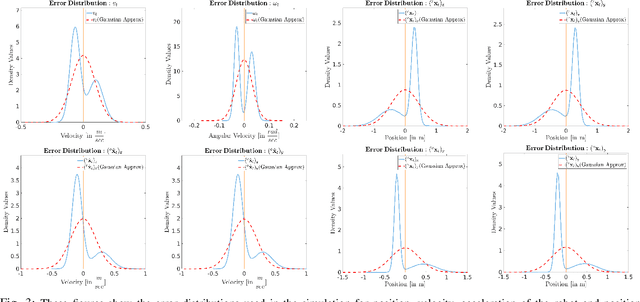
We consider the problem of an agent/robot with non-holonomic kinematics avoiding many dynamic obstacles. State and velocity noise of both the robot and obstacles as well as the robot's control noise are modelled as non-parametric distributions as often the Gaussian assumptions of noise models are violated in real-world scenarios. Under these assumptions, we formulate a robust MPC that samples robotic controls effectively in a manner that aligns the robot to the goal state while avoiding obstacles under the duress of such non-parametric noise. In particular, the MPC incorporates a distribution matching cost that effectively aligns the distribution of the current collision cone to a certain desired distribution whose samples are collision-free. This cost is posed as a distance function in the Hilbert Space, whose minimization typically results in the collision cone samples becoming collision-free. We compare and show tangible performance gain with methods that model the collision cone distribution by linearizing the Gaussian approximations of the original non-parametric state and obstacle distributions. We also show superior performance with methods that pose a chance constraint formulation of the Gaussian approximations of non-parametric noise without subjecting such approximations to further linearizations. The performance gain is shown both in terms of trajectory length and control costs that vindicates the efficacy of the proposed method. To the best of our knowledge, this is the first presentation of non-holonomic collision avoidance of moving obstacles in the presence of non-parametric state, velocity and actuator noise models.

Multi-Modal Model Predictive Control through Batch Non-Holonomic Trajectory Optimization: Application to Highway Driving

Standard Model Predictive Control (MPC) or trajectory optimization approaches perform only a local search to solve a complex non-convex optimization problem. As a result, they cannot capture the multi-modal characteristic of human driving. A global optimizer can be a potential solution but is computationally intractable in a real-time setting. In this paper, we present a real-time MPC capable of searching over different driving modalities. Our basic idea is simple: we run several goal-directed parallel trajectory optimizations and score the resulting trajectories based on user-defined meta cost functions. This allows us to perform a global search over several locally optimal motion plans. Although conceptually straightforward, realizing this idea in real-time with existing optimizers is highly challenging from technical and computational standpoints. With this motivation, we present a novel batch non-holonomic trajectory optimization whose underlying matrix algebra is easily parallelizable across problem instances and reduces to computing large batch matrix-vector products. This structure, in turn, is achieved by deriving a linearization-free multi-convex reformulation of the non-holonomic kinematics and collision avoidance constraints. We extensively validate our approach using both synthetic and real data sets (NGSIM) of traffic scenarios. We highlight how our algorithm automatically takes lane-change and overtaking decisions based on the defined meta cost function. Our batch optimizer achieves trajectories with lower meta cost, up to 6x faster than competing baselines.