Synthetic Data-Based Simulators for Recommender Systems: A Survey

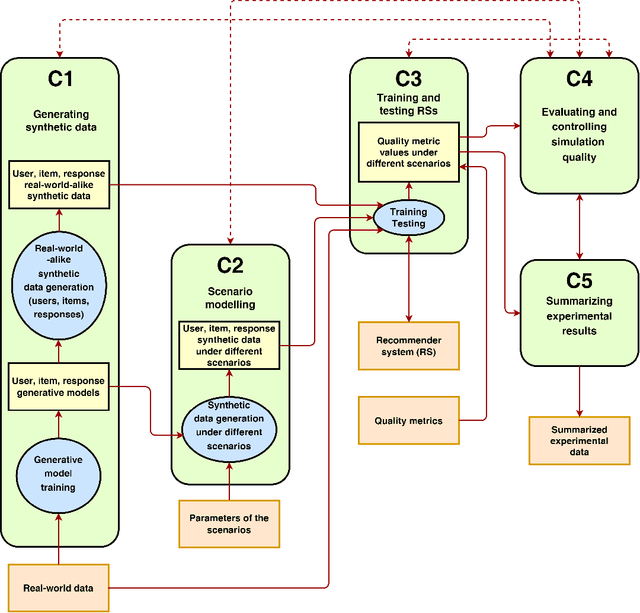
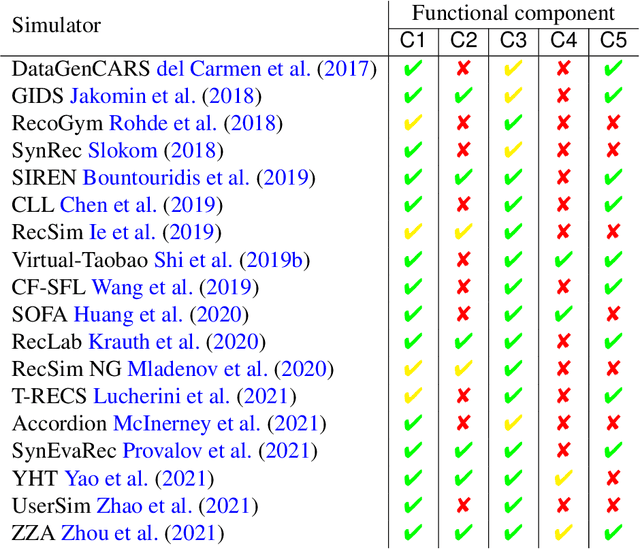
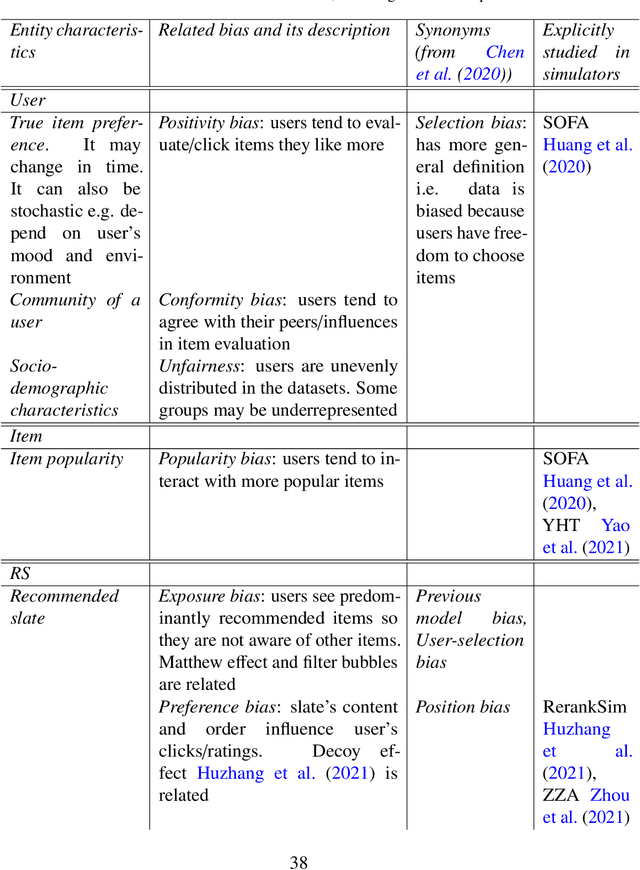
This survey aims at providing a comprehensive overview of the recent trends in the field of modeling and simulation (M&S) of interactions between users and recommender systems and applications of the M&S to the performance improvement of industrial recommender engines. We start with the motivation behind the development of frameworks implementing the simulations -- simulators -- and the usage of them for training and testing recommender systems of different types (including Reinforcement Learning ones). Furthermore, we provide a new consistent classification of existing simulators based on their functionality, approbation, and industrial effectiveness and moreover make a summary of the simulators found in the research literature. Besides other things, we discuss the building blocks of simulators: methods for synthetic data (user, item, user-item responses) generation, methods for what-if experimental analysis, methods and datasets used for simulation quality evaluation (including the methods that monitor and/or close possible simulation-to-reality gaps), and methods for summarization of experimental simulation results. Finally, this survey considers emerging topics and open problems in the field.

Federated Multi-view Matrix Factorization for Personalized Recommendations

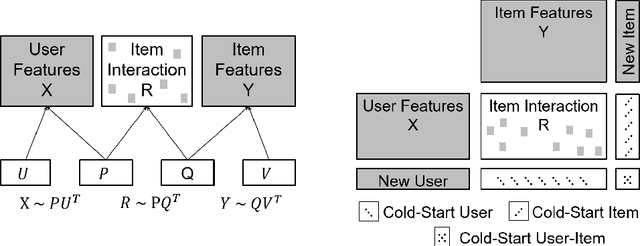
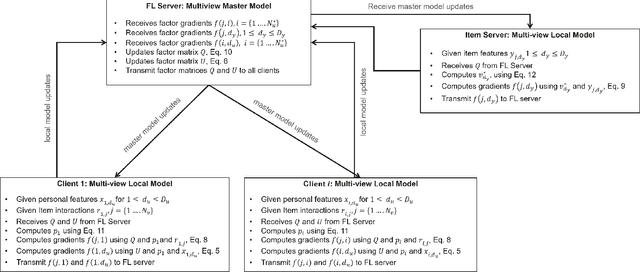
We introduce the federated multi-view matrix factorization method that extends the federated learning framework to matrix factorization with multiple data sources. Our method is able to learn the multi-view model without transferring the user's personal data to a central server. As far as we are aware this is the first federated model to provide recommendations using multi-view matrix factorization. The model is rigorously evaluated on three datasets on production settings. Empirical validation confirms that federated multi-view matrix factorization outperforms simpler methods that do not take into account the multi-view structure of the data, in addition, it demonstrates the usefulness of the proposed method for the challenging prediction tasks of cold-start federated recommendations.

State Space Gaussian Processes with Non-Gaussian Likelihood

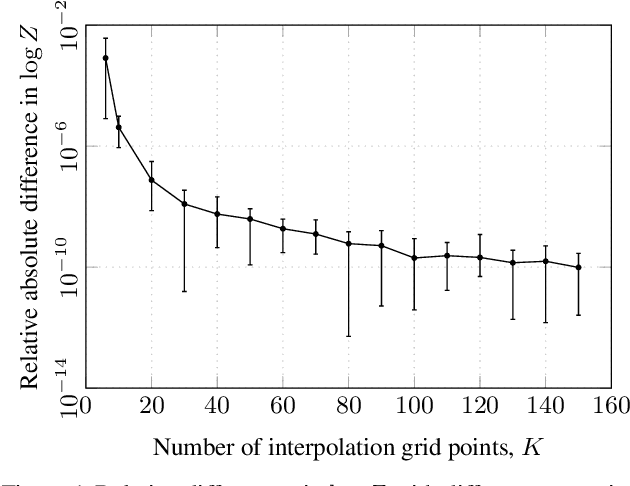
We provide a comprehensive overview and tooling for GP modeling with non-Gaussian likelihoods using state space methods. The state space formulation allows for solving one-dimensional GP models in $\mathcal{O}(n)$ time and memory complexity. While existing literature has focused on the connection between GP regression and state space methods, the computational primitives allowing for inference using general likelihoods in combination with the Laplace approximation (LA), variational Bayes (VB), and assumed density filtering (ADF, a.k.a. single-sweep expectation propagation, EP) schemes has been largely overlooked. We present means of combining the efficient $\mathcal{O}(n)$ state space methodology with existing inference methods. We extend existing methods, and provide unifying code implementing all approaches.

Parallelizable sparse inverse formulation Gaussian processes (SpInGP)

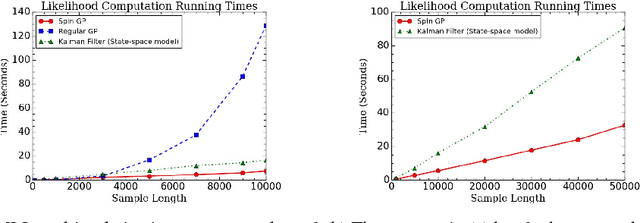
We propose a parallelizable sparse inverse formulation Gaussian process (SpInGP) for temporal models. It uses a sparse precision GP formulation and sparse matrix routines to speed up the computations. Due to the state-space formulation used in the algorithm, the time complexity of the basic SpInGP is linear, and because all the computations are parallelizable, the parallel form of the algorithm is sublinear in the number of data points. We provide example algorithms to implement the sparse matrix routines and experimentally test the method using both simulated and real data.

Gaussian Process Kernels for Popular State-Space Time Series Models

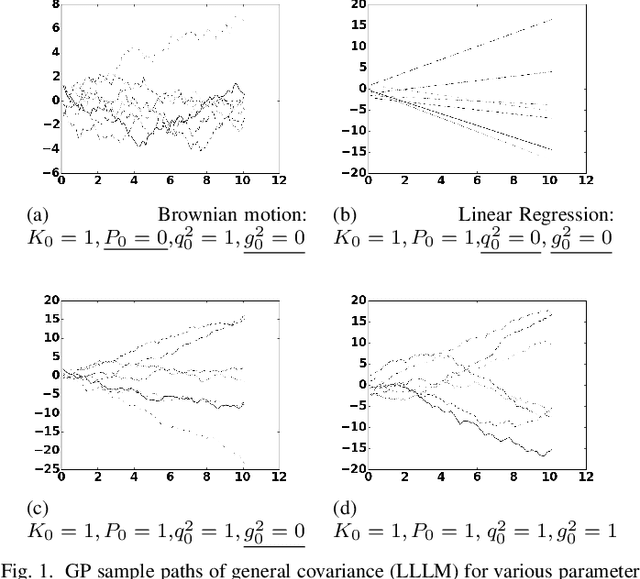
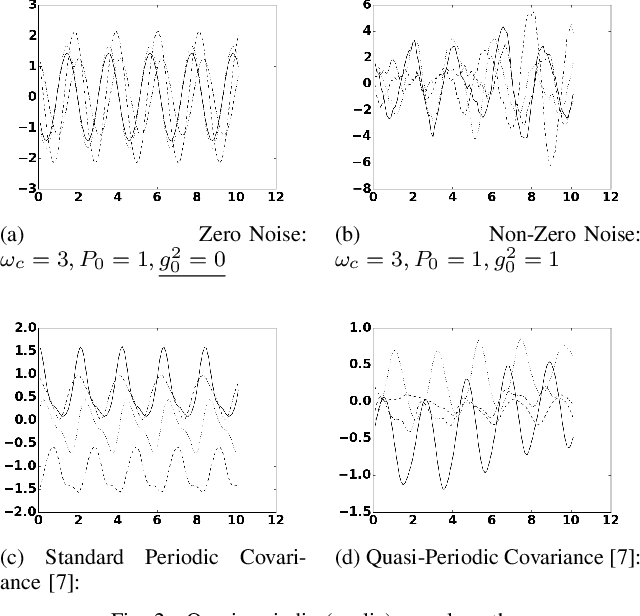
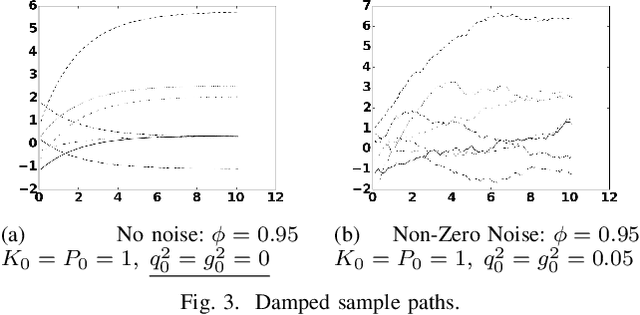
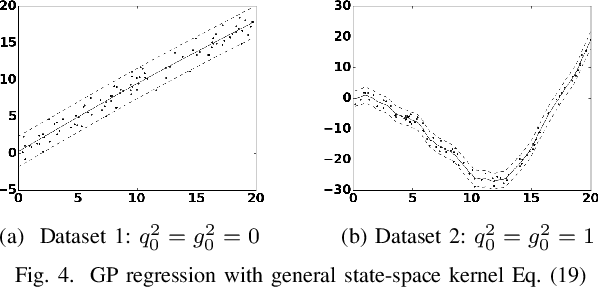
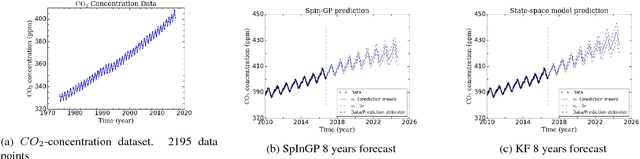
In this paper we investigate a link between state- space models and Gaussian Processes (GP) for time series modeling and forecasting. In particular, several widely used state- space models are transformed into continuous time form and corresponding Gaussian Process kernels are derived. Experimen- tal results demonstrate that the derived GP kernels are correct and appropriate for Gaussian Process Regression. An experiment with a real world dataset shows that the modeling is identical with state-space models and with the proposed GP kernels. The considered connection allows the researchers to look at their models from a different angle and facilitate sharing ideas between these two different modeling approaches.