Parallelizable sparse inverse formulation Gaussian processes (SpInGP)
Paper and Code
Sep 28, 2017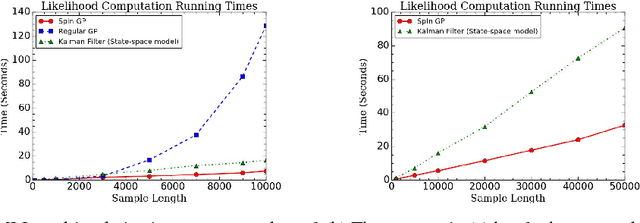
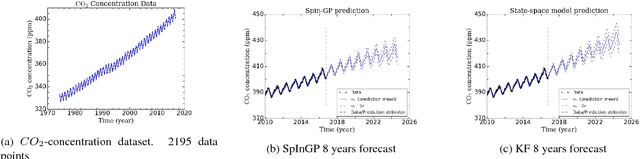
We propose a parallelizable sparse inverse formulation Gaussian process (SpInGP) for temporal models. It uses a sparse precision GP formulation and sparse matrix routines to speed up the computations. Due to the state-space formulation used in the algorithm, the time complexity of the basic SpInGP is linear, and because all the computations are parallelizable, the parallel form of the algorithm is sublinear in the number of data points. We provide example algorithms to implement the sparse matrix routines and experimentally test the method using both simulated and real data.
* Presented at Machine Learning in Signal Processing (MLSP2017)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge