Gaussian Process Kernels for Popular State-Space Time Series Models
Paper and Code
Oct 25, 2016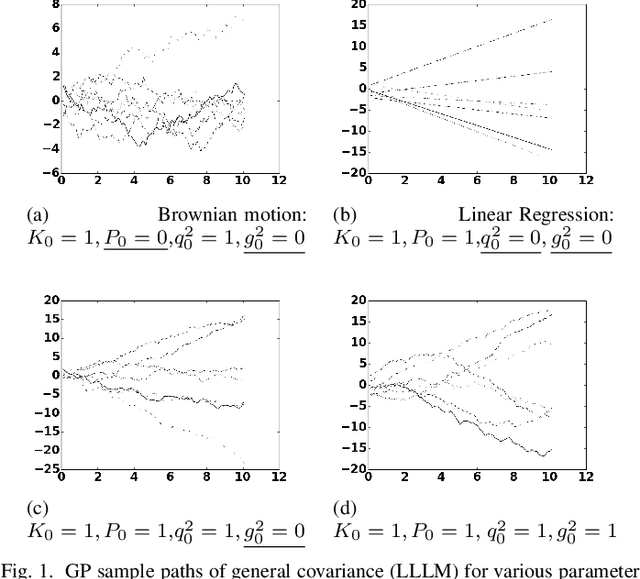
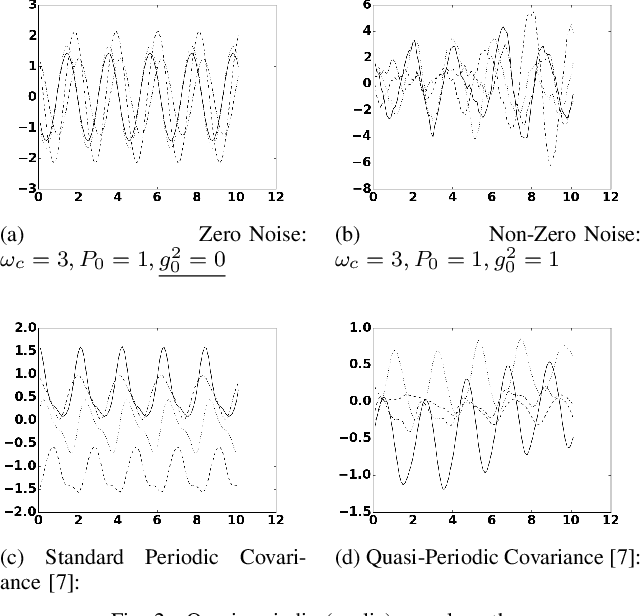
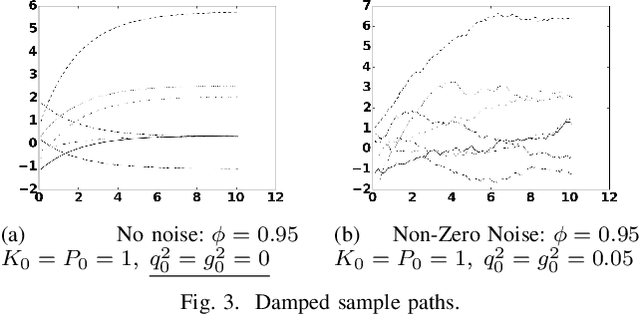
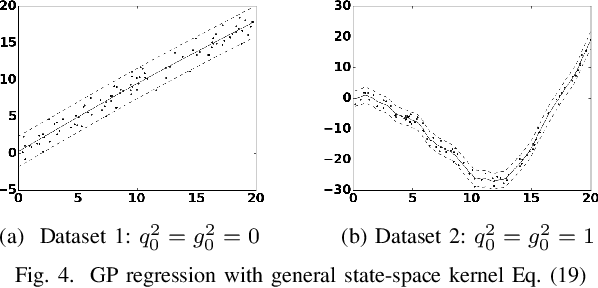
In this paper we investigate a link between state- space models and Gaussian Processes (GP) for time series modeling and forecasting. In particular, several widely used state- space models are transformed into continuous time form and corresponding Gaussian Process kernels are derived. Experimen- tal results demonstrate that the derived GP kernels are correct and appropriate for Gaussian Process Regression. An experiment with a real world dataset shows that the modeling is identical with state-space models and with the proposed GP kernels. The considered connection allows the researchers to look at their models from a different angle and facilitate sharing ideas between these two different modeling approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge