Rate distortion optimization over large scale video corpus with machine learning

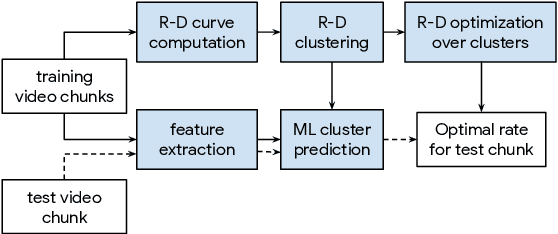
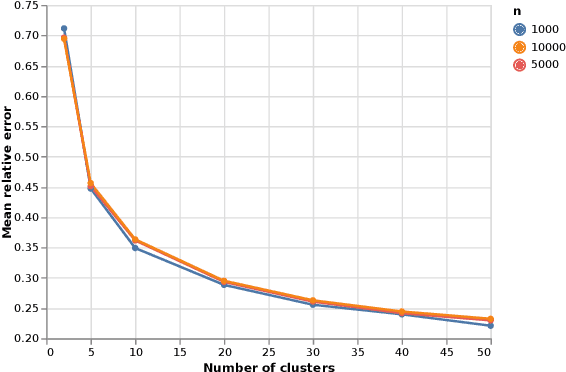
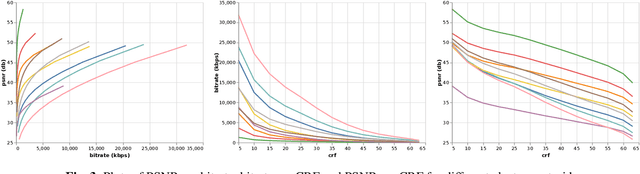
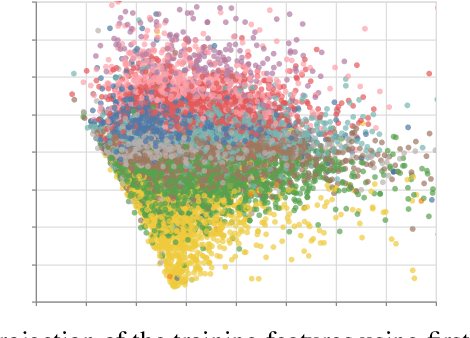
We present an efficient codec-agnostic method for bitrate allocation over a large scale video corpus with the goal of minimizing the average bitrate subject to constraints on average and minimum quality. Our method clusters the videos in the corpus such that videos within one cluster have similar rate-distortion (R-D) characteristics. We train a support vector machine classifier to predict the R-D cluster of a video using simple video complexity features that are computationally easy to obtain. The model allows us to classify a large sample of the corpus in order to estimate the distribution of the number of videos in each of the clusters. We use this distribution to find the optimal encoder operating point for each R-D cluster. Experiments with AV1 encoder show that our method can achieve the same average quality over the corpus with $22\%$ less average bitrate.

Guided Signal Reconstruction Theory

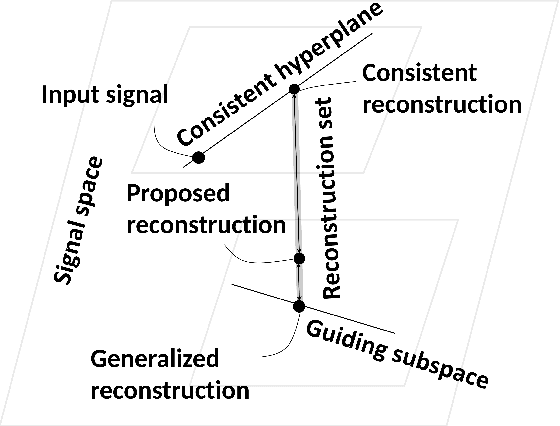
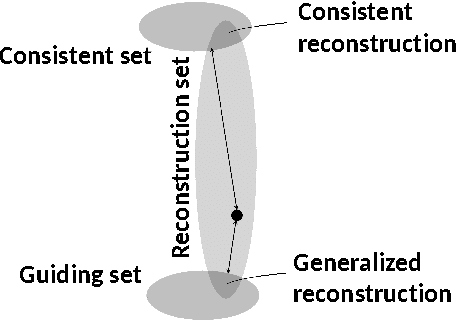
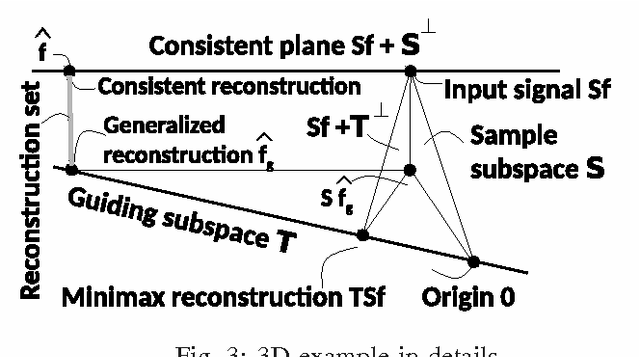
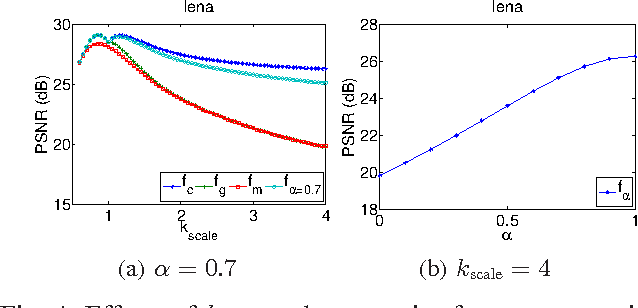
An axiomatic approach to signal reconstruction is formulated, involving a sample consistent set and a guiding set, describing desired reconstructions. New frame-less reconstruction methods are proposed, based on a novel concept of a reconstruction set, defined as a shortest pathway between the sample consistent set and the guiding set. Existence and uniqueness of the reconstruction set are investigated in a Hilbert space, where the guiding set is a closed subspace and the sample consistent set is a closed plane, formed by a sampling subspace. Connections to earlier known consistent, generalized, and regularized reconstructions are clarified. New stability and reconstruction error bounds are derived, using the largest nontrivial angle between the sampling and guiding subspaces. Conjugate gradient iterative reconstruction algorithms are proposed and illustrated numerically for image magnification.

Active Learning On Weighted Graphs Using Adaptive And Non-adaptive Approaches

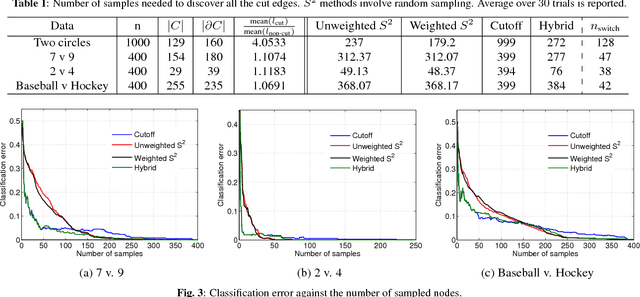
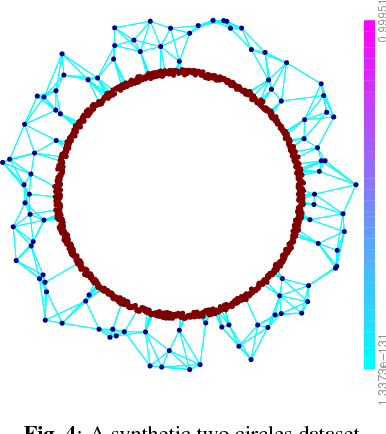
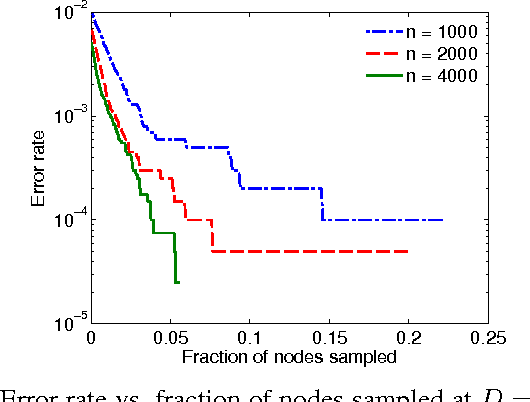
This paper studies graph-based active learning, where the goal is to reconstruct a binary signal defined on the nodes of a weighted graph, by sampling it on a small subset of the nodes. A new sampling algorithm is proposed, which sequentially selects the graph nodes to be sampled, based on an aggressive search for the boundary of the signal over the graph. The algorithm generalizes a recent method for sampling nodes in unweighted graphs. The generalization improves the sampling performance using the information gained from the available graph weights. An analysis of the number of samples required by the proposed algorithm is provided, and the gain over the unweighted method is further demonstrated in simulations. Additionally, the proposed method is compared with an alternative state of-the-art method, which is based on the graph's spectral properties. It is shown that the proposed method significantly outperforms the spectral sampling method, if the signal needs to be predicted with high accuracy. On the other hand, if a higher level of inaccuracy is tolerable, then the spectral method outperforms the proposed aggressive search method. Consequently, we propose a hybrid method, which is shown to combine the advantages of both approaches.

Active Learning for Community Detection in Stochastic Block Models

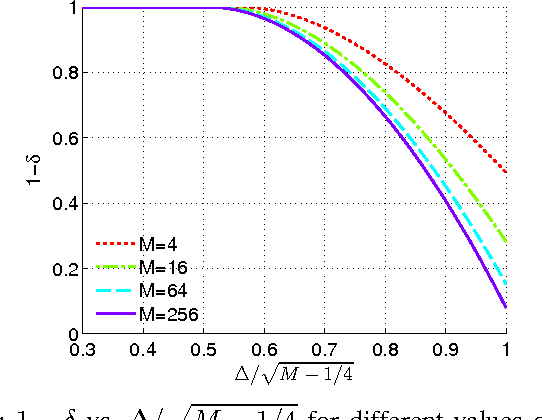
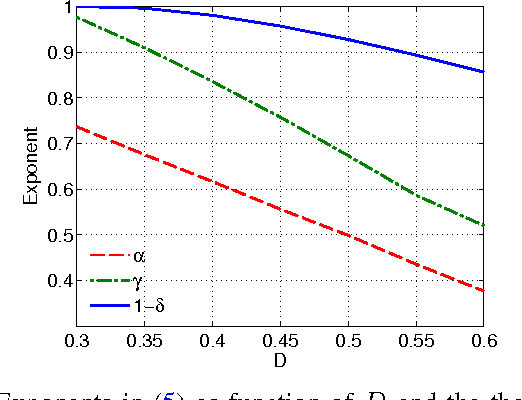
The stochastic block model (SBM) is an important generative model for random graphs in network science and machine learning, useful for benchmarking community detection (or clustering) algorithms. The symmetric SBM generates a graph with $2n$ nodes which cluster into two equally sized communities. Nodes connect with probability $p$ within a community and $q$ across different communities. We consider the case of $p=a\ln (n)/n$ and $q=b\ln (n)/n$. In this case, it was recently shown that recovering the community membership (or label) of every node with high probability (w.h.p.) using only the graph is possible if and only if the Chernoff-Hellinger (CH) divergence $D(a,b)=(\sqrt{a}-\sqrt{b})^2 \geq 1$. In this work, we study if, and by how much, community detection below the clustering threshold (i.e. $D(a,b)<1$) is possible by querying the labels of a limited number of chosen nodes (i.e., active learning). Our main result is to show that, under certain conditions, sampling the labels of a vanishingly small fraction of nodes (a number sub-linear in $n$) is sufficient for exact community detection even when $D(a,b)<1$. Furthermore, we provide an efficient learning algorithm which recovers the community memberships of all nodes w.h.p. as long as the number of sampled points meets the sufficient condition. We also show that recovery is not possible if the number of observed labels is less than $n^{1-D(a,b)}$. The validity of our results is demonstrated through numerical experiments.

A Probabilistic Interpretation of Sampling Theory of Graph Signals

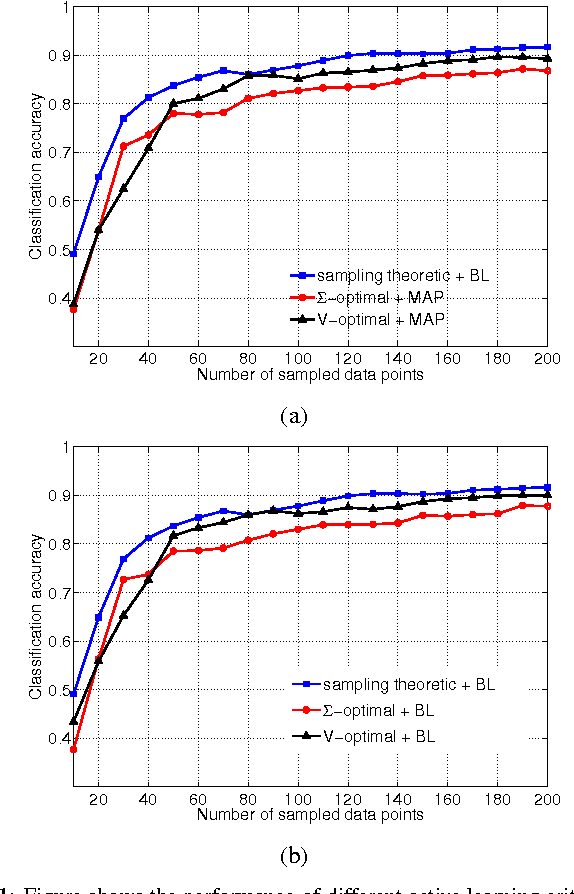
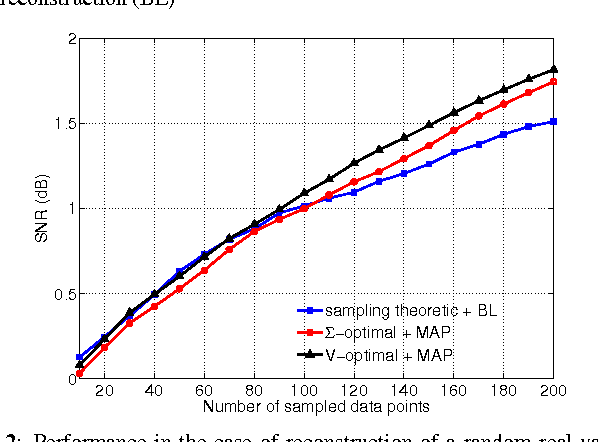
We give a probabilistic interpretation of sampling theory of graph signals. To do this, we first define a generative model for the data using a pairwise Gaussian random field (GRF) which depends on the graph. We show that, under certain conditions, reconstructing a graph signal from a subset of its samples by least squares is equivalent to performing MAP inference on an approximation of this GRF which has a low rank covariance matrix. We then show that a sampling set of given size with the largest associated cut-off frequency, which is optimal from a sampling theoretic point of view, minimizes the worst case predictive covariance of the MAP estimate on the GRF. This interpretation also gives an intuitive explanation for the superior performance of the sampling theoretic approach to active semi-supervised classification.

Active Semi-Supervised Learning Using Sampling Theory for Graph Signals

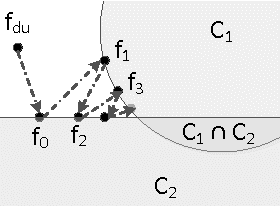
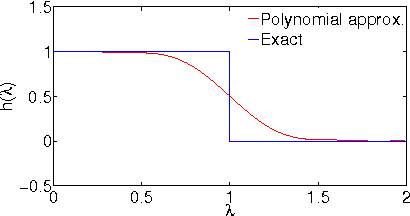
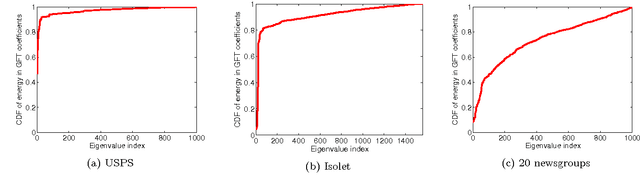
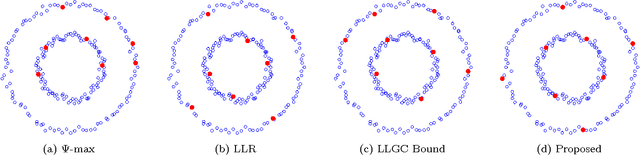
We consider the problem of offline, pool-based active semi-supervised learning on graphs. This problem is important when the labeled data is scarce and expensive whereas unlabeled data is easily available. The data points are represented by the vertices of an undirected graph with the similarity between them captured by the edge weights. Given a target number of nodes to label, the goal is to choose those nodes that are most informative and then predict the unknown labels. We propose a novel framework for this problem based on our recent results on sampling theory for graph signals. A graph signal is a real-valued function defined on each node of the graph. A notion of frequency for such signals can be defined using the spectrum of the graph Laplacian matrix. The sampling theory for graph signals aims to extend the traditional Nyquist-Shannon sampling theory by allowing us to identify the class of graph signals that can be reconstructed from their values on a subset of vertices. This approach allows us to define a criterion for active learning based on sampling set selection which aims at maximizing the frequency of the signals that can be reconstructed from their samples on the set. Experiments show the effectiveness of our method.

Localized Iterative Methods for Interpolation in Graph Structured Data

In this paper, we present two localized graph filtering based methods for interpolating graph signals defined on the vertices of arbitrary graphs from only a partial set of samples. The first method is an extension of previous work on reconstructing bandlimited graph signals from partially observed samples. The iterative graph filtering approach very closely approximates the solution proposed in the that work, while being computationally more efficient. As an alternative, we propose a regularization based framework in which we define the cost of reconstruction to be a combination of smoothness of the graph signal and the reconstruction error with respect to the known samples, and find solutions that minimize this cost. We provide both a closed form solution and a computationally efficient iterative solution of the optimization problem. The experimental results on the recommendation system datasets demonstrate effectiveness of the proposed methods.

Bilateral Filter: Graph Spectral Interpretation and Extensions

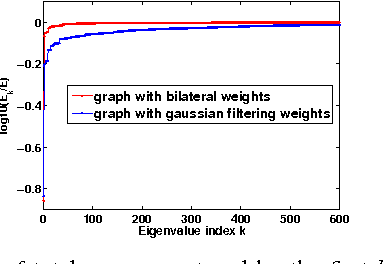
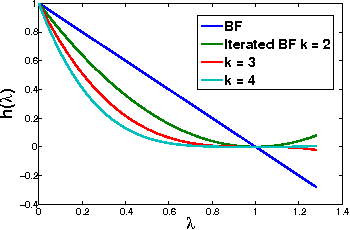
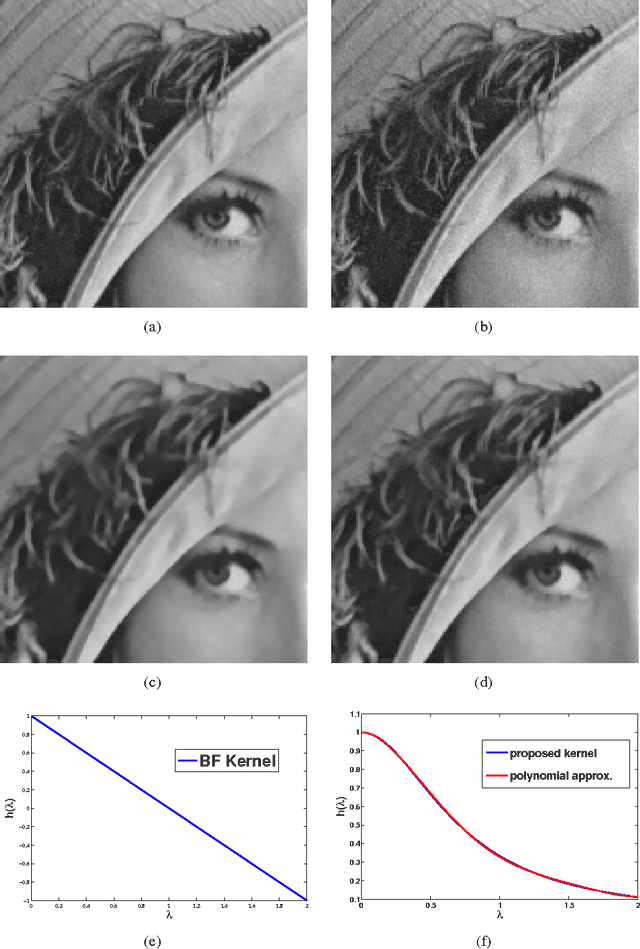
In this paper we study the bilateral filter proposed by Tomasi and Manduchi, as a spectral domain transform defined on a weighted graph. The nodes of this graph represent the pixels in the image and a graph signal defined on the nodes represents the intensity values. Edge weights in the graph correspond to the bilateral filter coefficients and hence are data adaptive. Spectrum of a graph is defined in terms of the eigenvalues and eigenvectors of the graph Laplacian matrix. We use this spectral interpretation to generalize the bilateral filter and propose more flexible and application specific spectral designs of bilateral-like filters. We show that these spectral filters can be implemented with k-iterative bilateral filtering operations and do not require expensive diagonalization of the Laplacian matrix.