Active Learning On Weighted Graphs Using Adaptive And Non-adaptive Approaches
Paper and Code
May 18, 2016
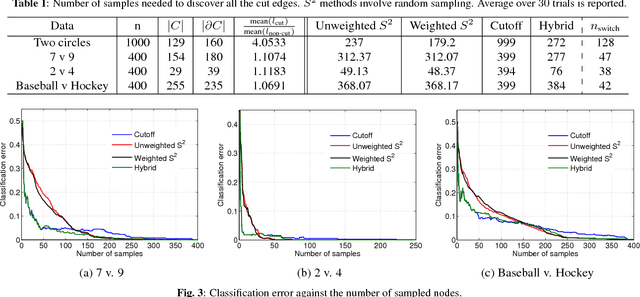
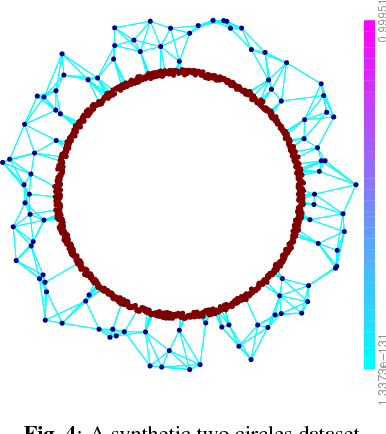
This paper studies graph-based active learning, where the goal is to reconstruct a binary signal defined on the nodes of a weighted graph, by sampling it on a small subset of the nodes. A new sampling algorithm is proposed, which sequentially selects the graph nodes to be sampled, based on an aggressive search for the boundary of the signal over the graph. The algorithm generalizes a recent method for sampling nodes in unweighted graphs. The generalization improves the sampling performance using the information gained from the available graph weights. An analysis of the number of samples required by the proposed algorithm is provided, and the gain over the unweighted method is further demonstrated in simulations. Additionally, the proposed method is compared with an alternative state of-the-art method, which is based on the graph's spectral properties. It is shown that the proposed method significantly outperforms the spectral sampling method, if the signal needs to be predicted with high accuracy. On the other hand, if a higher level of inaccuracy is tolerable, then the spectral method outperforms the proposed aggressive search method. Consequently, we propose a hybrid method, which is shown to combine the advantages of both approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge