Active Learning On Weighted Graphs Using Adaptive And Non-adaptive Approaches

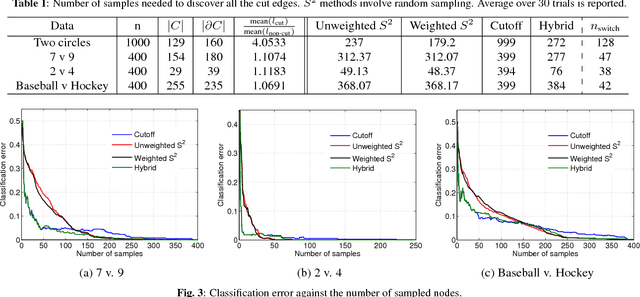
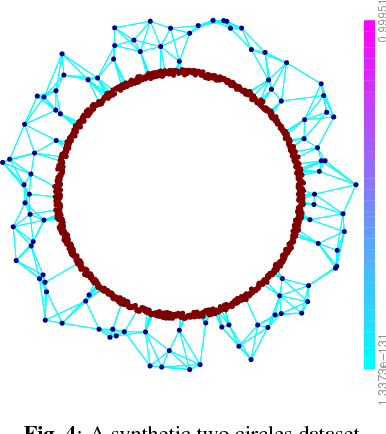
This paper studies graph-based active learning, where the goal is to reconstruct a binary signal defined on the nodes of a weighted graph, by sampling it on a small subset of the nodes. A new sampling algorithm is proposed, which sequentially selects the graph nodes to be sampled, based on an aggressive search for the boundary of the signal over the graph. The algorithm generalizes a recent method for sampling nodes in unweighted graphs. The generalization improves the sampling performance using the information gained from the available graph weights. An analysis of the number of samples required by the proposed algorithm is provided, and the gain over the unweighted method is further demonstrated in simulations. Additionally, the proposed method is compared with an alternative state of-the-art method, which is based on the graph's spectral properties. It is shown that the proposed method significantly outperforms the spectral sampling method, if the signal needs to be predicted with high accuracy. On the other hand, if a higher level of inaccuracy is tolerable, then the spectral method outperforms the proposed aggressive search method. Consequently, we propose a hybrid method, which is shown to combine the advantages of both approaches.

Active Learning for Community Detection in Stochastic Block Models

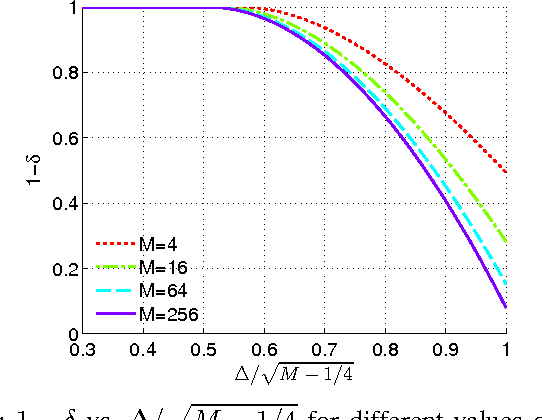
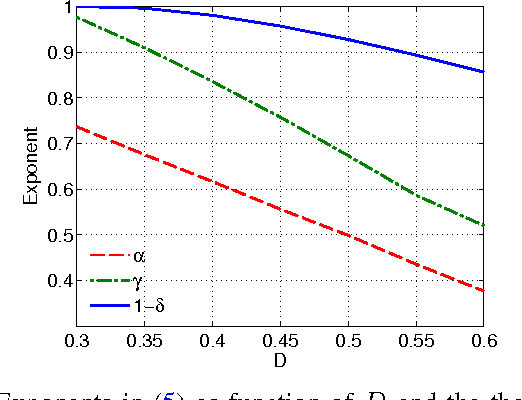
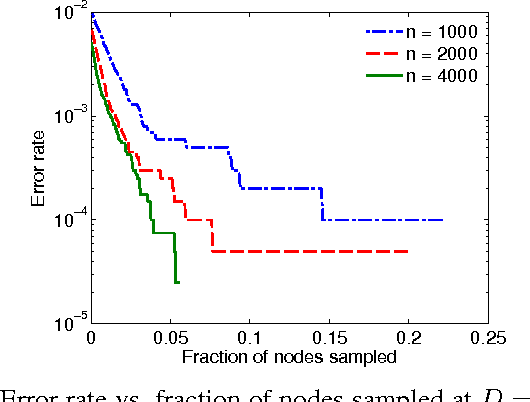
The stochastic block model (SBM) is an important generative model for random graphs in network science and machine learning, useful for benchmarking community detection (or clustering) algorithms. The symmetric SBM generates a graph with $2n$ nodes which cluster into two equally sized communities. Nodes connect with probability $p$ within a community and $q$ across different communities. We consider the case of $p=a\ln (n)/n$ and $q=b\ln (n)/n$. In this case, it was recently shown that recovering the community membership (or label) of every node with high probability (w.h.p.) using only the graph is possible if and only if the Chernoff-Hellinger (CH) divergence $D(a,b)=(\sqrt{a}-\sqrt{b})^2 \geq 1$. In this work, we study if, and by how much, community detection below the clustering threshold (i.e. $D(a,b)<1$) is possible by querying the labels of a limited number of chosen nodes (i.e., active learning). Our main result is to show that, under certain conditions, sampling the labels of a vanishingly small fraction of nodes (a number sub-linear in $n$) is sufficient for exact community detection even when $D(a,b)<1$. Furthermore, we provide an efficient learning algorithm which recovers the community memberships of all nodes w.h.p. as long as the number of sampled points meets the sufficient condition. We also show that recovery is not possible if the number of observed labels is less than $n^{1-D(a,b)}$. The validity of our results is demonstrated through numerical experiments.