Active Learning for Community Detection in Stochastic Block Models
Paper and Code
May 08, 2016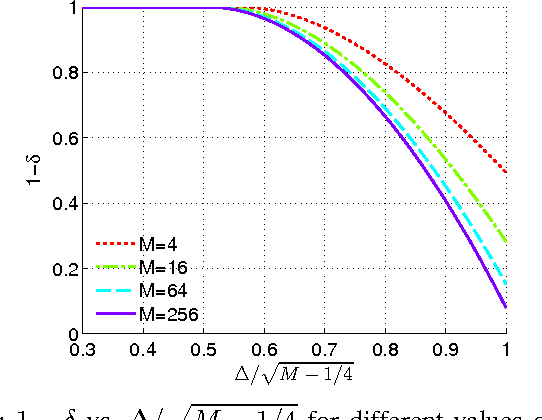
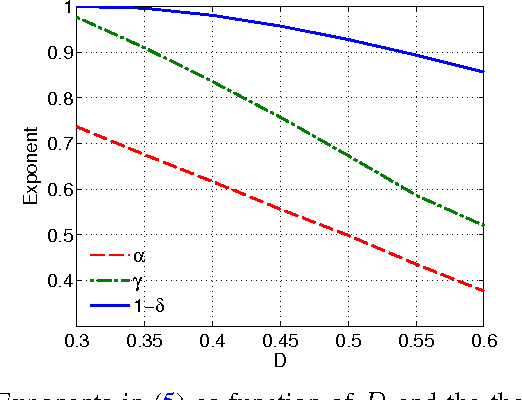
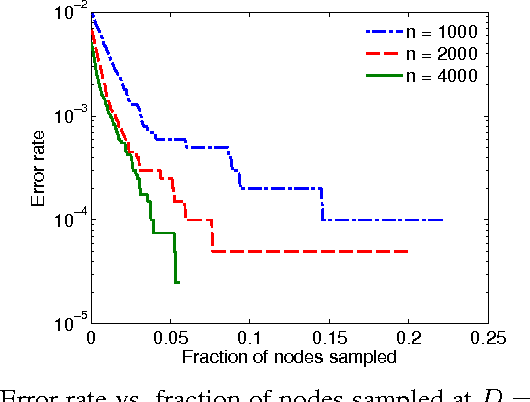
The stochastic block model (SBM) is an important generative model for random graphs in network science and machine learning, useful for benchmarking community detection (or clustering) algorithms. The symmetric SBM generates a graph with $2n$ nodes which cluster into two equally sized communities. Nodes connect with probability $p$ within a community and $q$ across different communities. We consider the case of $p=a\ln (n)/n$ and $q=b\ln (n)/n$. In this case, it was recently shown that recovering the community membership (or label) of every node with high probability (w.h.p.) using only the graph is possible if and only if the Chernoff-Hellinger (CH) divergence $D(a,b)=(\sqrt{a}-\sqrt{b})^2 \geq 1$. In this work, we study if, and by how much, community detection below the clustering threshold (i.e. $D(a,b)<1$) is possible by querying the labels of a limited number of chosen nodes (i.e., active learning). Our main result is to show that, under certain conditions, sampling the labels of a vanishingly small fraction of nodes (a number sub-linear in $n$) is sufficient for exact community detection even when $D(a,b)<1$. Furthermore, we provide an efficient learning algorithm which recovers the community memberships of all nodes w.h.p. as long as the number of sampled points meets the sufficient condition. We also show that recovery is not possible if the number of observed labels is less than $n^{1-D(a,b)}$. The validity of our results is demonstrated through numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge