Preconditioned Spectral Clustering for Stochastic Block Partition Streaming Graph Challenge

Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) is demonstrated to efficiently solve eigenvalue problems for graph Laplacians that appear in spectral clustering. For static graph partitioning, 10-20 iterations of LOBPCG without preconditioning result in ~10x error reduction, enough to achieve 100% correctness for all Challenge datasets with known truth partitions, e.g., for graphs with 5K/.1M (50K/1M) Vertices/Edges in 2 (7) seconds, compared to over 5,000 (30,000) seconds needed by the baseline Python code. Our Python code 100% correctly determines 98 (160) clusters from the Challenge static graphs with 0.5M (2M) vertices in 270 (1,700) seconds using 10GB (50GB) of memory. Our single-precision MATLAB code calculates the same clusters at half time and memory. For streaming graph partitioning, LOBPCG is initiated with approximate eigenvectors of the graph Laplacian already computed for the previous graph, in many cases reducing 2-3 times the number of required LOBPCG iterations, compared to the static case. Our spectral clustering is generic, i.e. assuming nothing specific of the block model or streaming, used to generate the graphs for the Challenge, in contrast to the base code. Nevertheless, in 10-stage streaming comparison with the base code for the 5K graph, the quality of our clusters is similar or better starting at stage 4 (7) for emerging edging (snowballing) streaming, while the computations are over 100-1000 faster.

Signal reconstruction via operator guiding

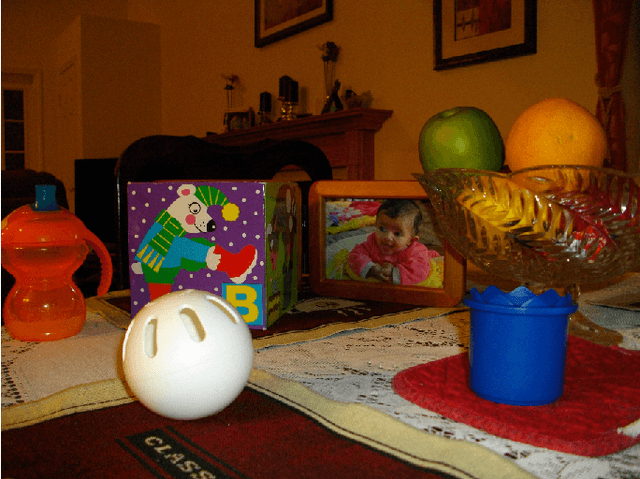
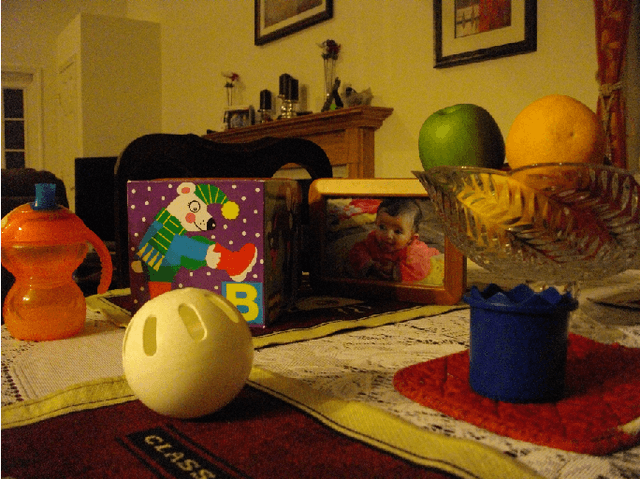
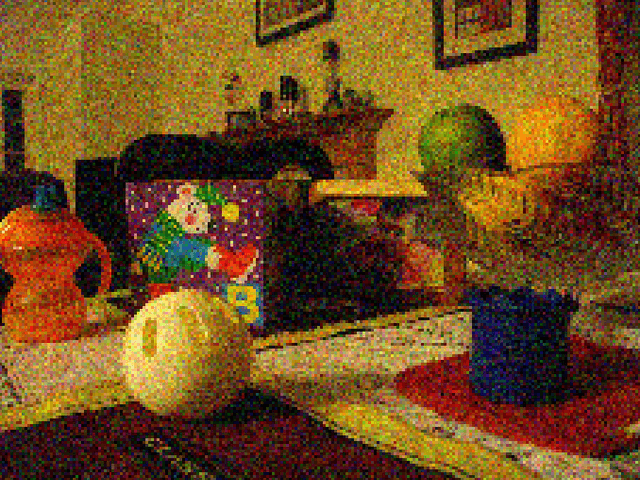
Signal reconstruction from a sample using an orthogonal projector onto a guiding subspace is theoretically well justified, but may be difficult to practically implement. We propose more general guiding operators, which increase signal components in the guiding subspace relative to those in a complementary subspace, e.g., iterative low-pass edge-preserving filters for super-resolution of images. Two examples of super-resolution illustrate our technology: a no-flash RGB photo guided using a high resolution flash RGB photo, and a depth image guided using a high resolution RGB photo.

Guided Signal Reconstruction Theory

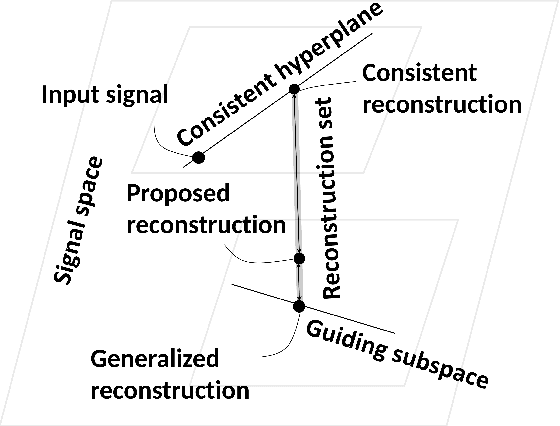
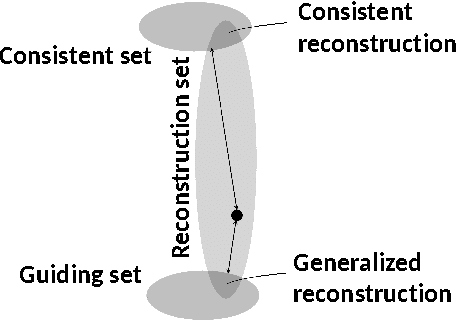
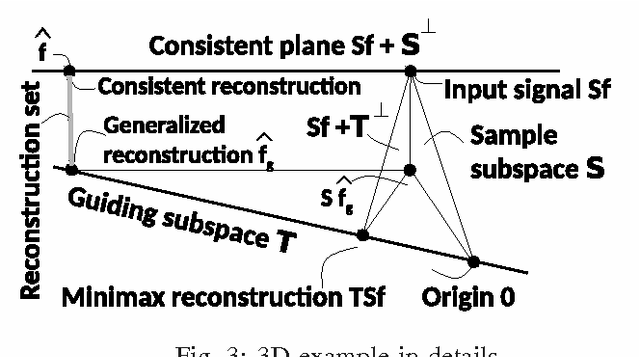
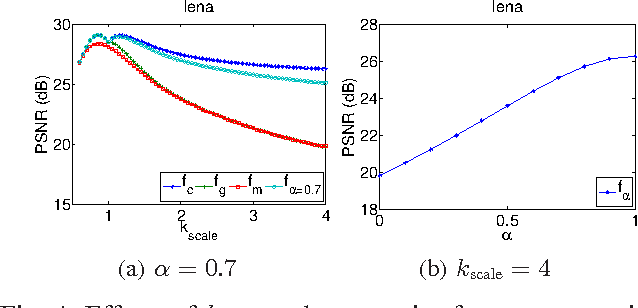
An axiomatic approach to signal reconstruction is formulated, involving a sample consistent set and a guiding set, describing desired reconstructions. New frame-less reconstruction methods are proposed, based on a novel concept of a reconstruction set, defined as a shortest pathway between the sample consistent set and the guiding set. Existence and uniqueness of the reconstruction set are investigated in a Hilbert space, where the guiding set is a closed subspace and the sample consistent set is a closed plane, formed by a sampling subspace. Connections to earlier known consistent, generalized, and regularized reconstructions are clarified. New stability and reconstruction error bounds are derived, using the largest nontrivial angle between the sampling and guiding subspaces. Conjugate gradient iterative reconstruction algorithms are proposed and illustrated numerically for image magnification.

Accelerated graph-based nonlinear denoising filters

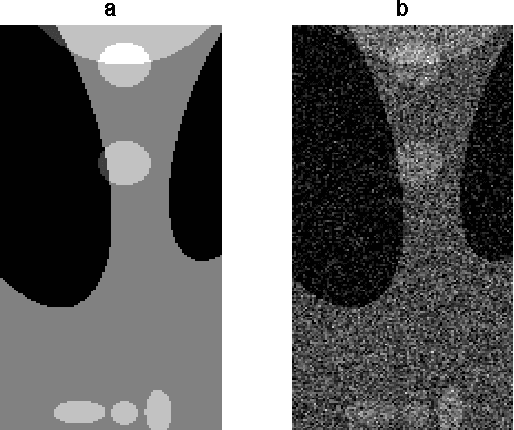
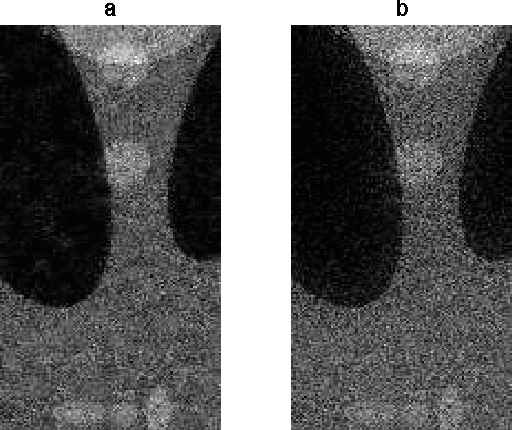
Denoising filters, such as bilateral, guided, and total variation filters, applied to images on general graphs may require repeated application if noise is not small enough. We formulate two acceleration techniques of the resulted iterations: conjugate gradient method and Nesterov's acceleration. We numerically show efficiency of the accelerated nonlinear filters for image denoising and demonstrate 2-12 times speed-up, i.e., the acceleration techniques reduce the number of iterations required to reach a given peak signal-to-noise ratio (PSNR) by the above indicated factor of 2-12.

Edge-enhancing Filters with Negative Weights

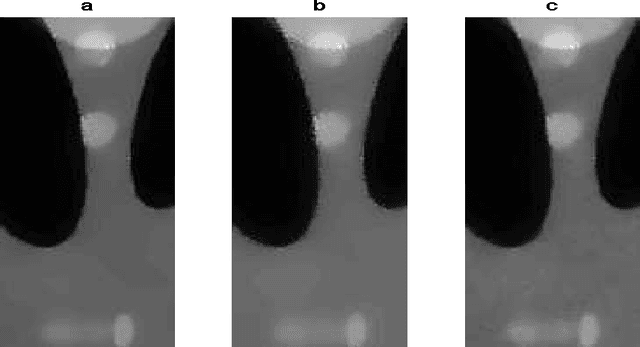
In [DOI:10.1109/ICMEW.2014.6890711], a graph-based denoising is performed by projecting the noisy image to a lower dimensional Krylov subspace of the graph Laplacian, constructed using nonnegative weights determined by distances between image data corresponding to image pixels. We~extend the construction of the graph Laplacian to the case, where some graph weights can be negative. Removing the positivity constraint provides a more accurate inference of a graph model behind the data, and thus can improve quality of filters for graph-based signal processing, e.g., denoising, compared to the standard construction, without affecting the costs.

Accelerated graph-based spectral polynomial filters

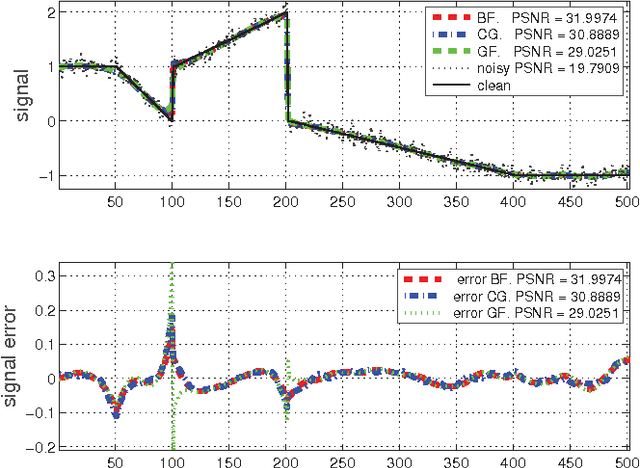
Graph-based spectral denoising is a low-pass filtering using the eigendecomposition of the graph Laplacian matrix of a noisy signal. Polynomial filtering avoids costly computation of the eigendecomposition by projections onto suitable Krylov subspaces. Polynomial filters can be based, e.g., on the bilateral and guided filters. We propose constructing accelerated polynomial filters by running flexible Krylov subspace based linear and eigenvalue solvers such as the Block Locally Optimal Preconditioned Conjugate Gradient (LOBPCG) method.

Chebyshev and Conjugate Gradient Filters for Graph Image Denoising

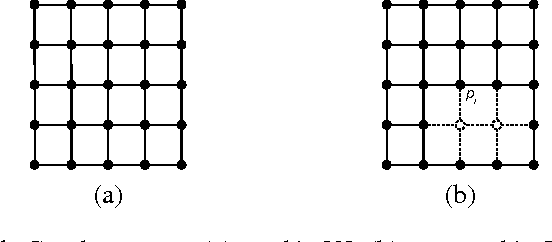
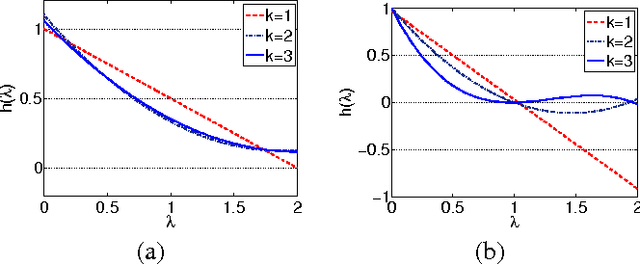
In 3D image/video acquisition, different views are often captured with varying noise levels across the views. In this paper, we propose a graph-based image enhancement technique that uses a higher quality view to enhance a degraded view. A depth map is utilized as auxiliary information to match the perspectives of the two views. Our method performs graph-based filtering of the noisy image by directly computing a projection of the image to be filtered onto a lower dimensional Krylov subspace of the graph Laplacian. We discuss two graph spectral denoising methods: first using Chebyshev polynomials, and second using iterations of the conjugate gradient algorithm. Our framework generalizes previously known polynomial graph filters, and we demonstrate through numerical simulations that our proposed technique produces subjectively cleaner images with about 1-3 dB improvement in PSNR over existing polynomial graph filters.

Conjugate Gradient Acceleration of Non-Linear Smoothing Filters

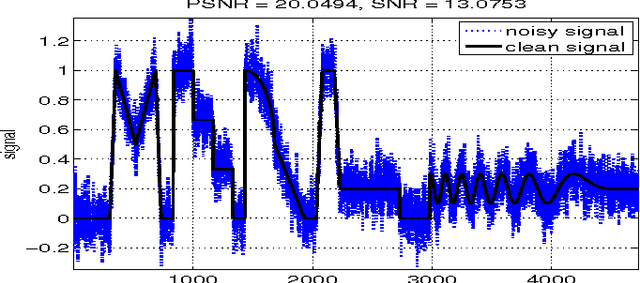
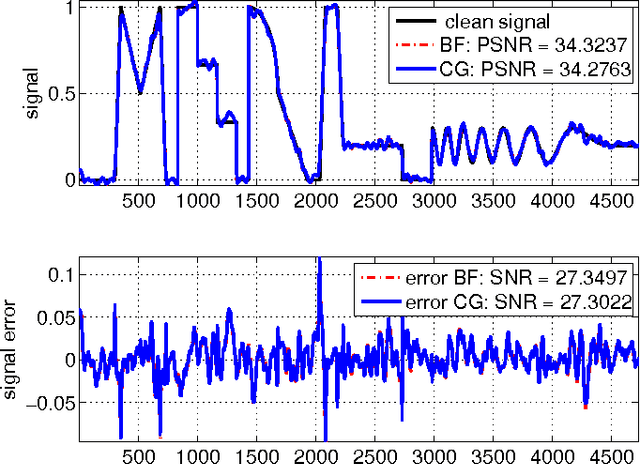
The most efficient signal edge-preserving smoothing filters, e.g., for denoising, are non-linear. Thus, their acceleration is challenging and is often performed in practice by tuning filter parameters, such as by increasing the width of the local smoothing neighborhood, resulting in more aggressive smoothing of a single sweep at the cost of increased edge blurring. We propose an alternative technology, accelerating the original filters without tuning, by running them through a special conjugate gradient method, not affecting their quality. The filter non-linearity is dealt with by careful freezing and restarting. Our initial numerical experiments on toy one-dimensional signals demonstrate 20x acceleration of the classical bilateral filter and 3-5x acceleration of the recently developed guided filter.