Signal reconstruction via operator guiding

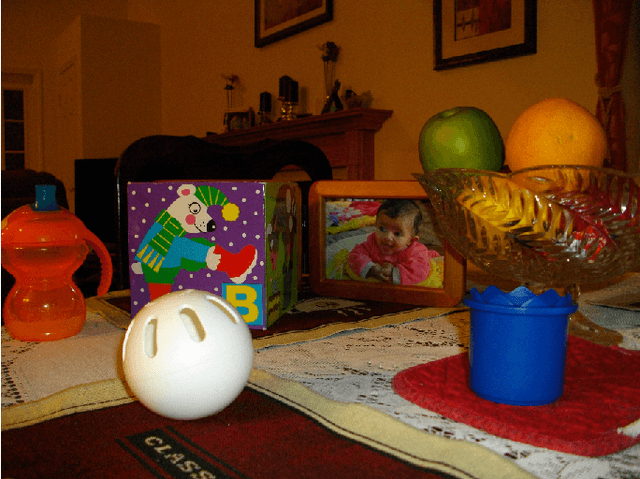
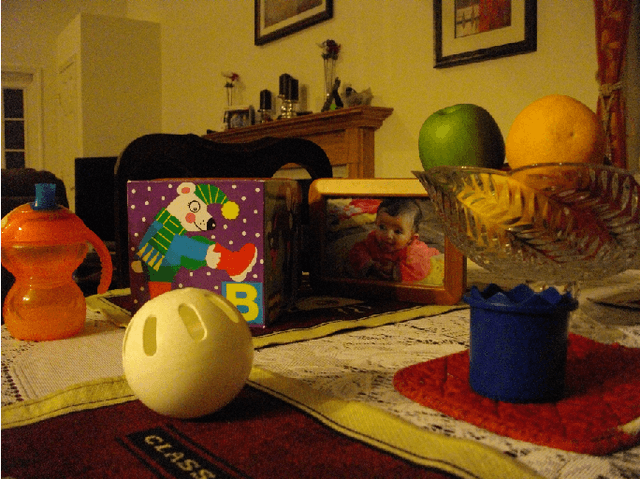
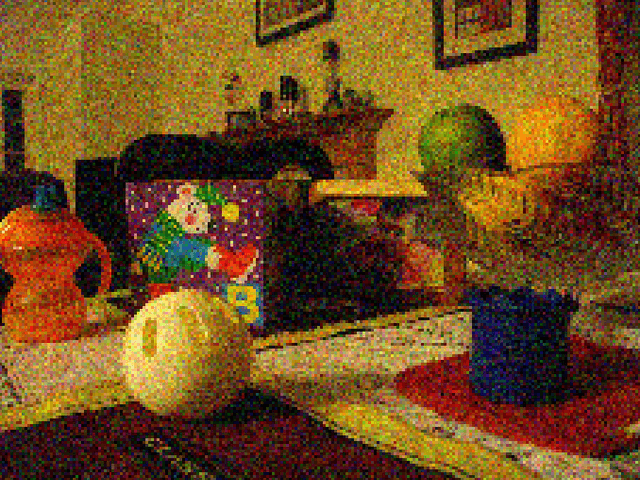
Signal reconstruction from a sample using an orthogonal projector onto a guiding subspace is theoretically well justified, but may be difficult to practically implement. We propose more general guiding operators, which increase signal components in the guiding subspace relative to those in a complementary subspace, e.g., iterative low-pass edge-preserving filters for super-resolution of images. Two examples of super-resolution illustrate our technology: a no-flash RGB photo guided using a high resolution flash RGB photo, and a depth image guided using a high resolution RGB photo.

Accelerated graph-based nonlinear denoising filters

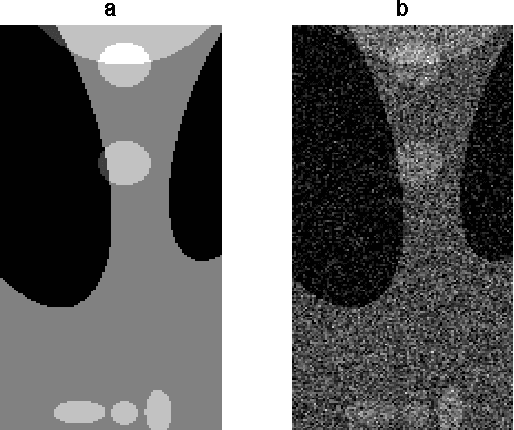
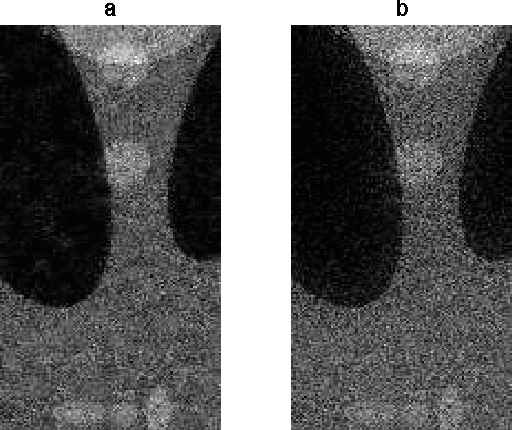
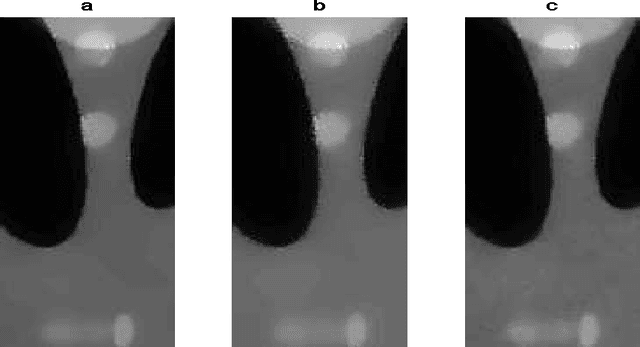
Denoising filters, such as bilateral, guided, and total variation filters, applied to images on general graphs may require repeated application if noise is not small enough. We formulate two acceleration techniques of the resulted iterations: conjugate gradient method and Nesterov's acceleration. We numerically show efficiency of the accelerated nonlinear filters for image denoising and demonstrate 2-12 times speed-up, i.e., the acceleration techniques reduce the number of iterations required to reach a given peak signal-to-noise ratio (PSNR) by the above indicated factor of 2-12.

Accelerated graph-based spectral polynomial filters

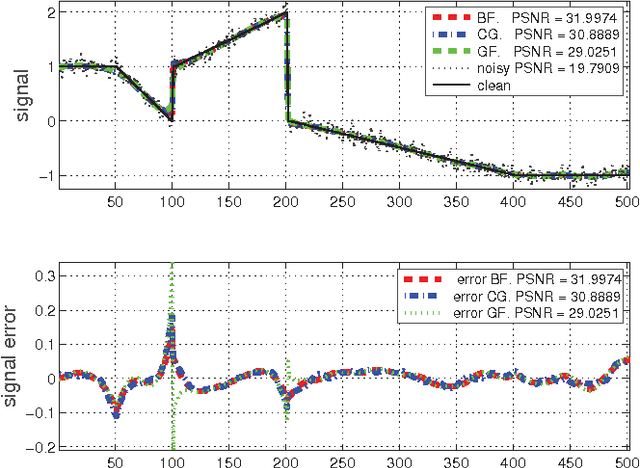
Graph-based spectral denoising is a low-pass filtering using the eigendecomposition of the graph Laplacian matrix of a noisy signal. Polynomial filtering avoids costly computation of the eigendecomposition by projections onto suitable Krylov subspaces. Polynomial filters can be based, e.g., on the bilateral and guided filters. We propose constructing accelerated polynomial filters by running flexible Krylov subspace based linear and eigenvalue solvers such as the Block Locally Optimal Preconditioned Conjugate Gradient (LOBPCG) method.

Conjugate Gradient Acceleration of Non-Linear Smoothing Filters

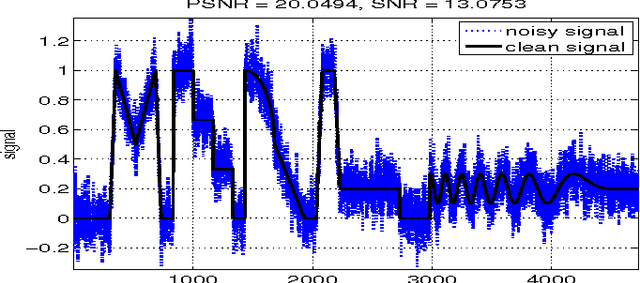
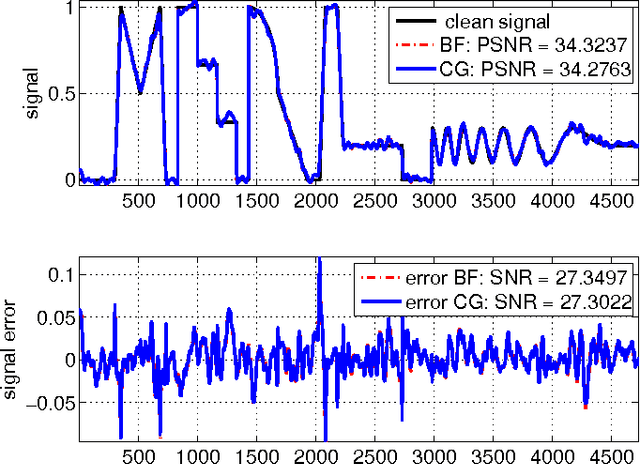
The most efficient signal edge-preserving smoothing filters, e.g., for denoising, are non-linear. Thus, their acceleration is challenging and is often performed in practice by tuning filter parameters, such as by increasing the width of the local smoothing neighborhood, resulting in more aggressive smoothing of a single sweep at the cost of increased edge blurring. We propose an alternative technology, accelerating the original filters without tuning, by running them through a special conjugate gradient method, not affecting their quality. The filter non-linearity is dealt with by careful freezing and restarting. Our initial numerical experiments on toy one-dimensional signals demonstrate 20x acceleration of the classical bilateral filter and 3-5x acceleration of the recently developed guided filter.